「こんなときどう教えればいいの?」「授業のここでいつも悩む。」「学習指導要領のことをもっと知りたい!」そんな先生方の疑問やお悩みなどにお答えします。
質問投稿フォームはこちら
Q
授業で、具体物を操作させるのと、端末の画面上で操作させるのとでは、どちらが良いですか。
2023.1.31 / 授業の進め方
回答者:近畿大学附属小学校 教諭 外山宏行
A
前出の文部科学省の資料においても、ICT活用にあたっての算数科の特質として、「具体的な体験を伴う学習等を通じて、児童に算数の論理を理解させることが大切」であるということが記されています。ここでいう「具体的な活動」とは、具体物を使った活動と、デジタル教材などを使ったシミュレーションの両方が想定できます。
具体物といっても、見せるだけなら動画の方が何度も繰り返し見ることができます。何度もやり直しをするなら、デジタルを使ったシミュレーションの方が効果的だと言えます。逆に、量感を伴うような活動は具体物なしには効果が期待できません。何でもかんでもデジタルにすれば良いというのではなく、ICTを効果的に活用することが重要とした上で、活用する場面を適切に選択することが重要です。
近畿大学附属小学校 教諭 外山宏行
Q
問題演習はデジタルドリルだけで十分ですか?
2023.1.31 / 授業の進め方
回答者:近畿大学附属小学校 教諭 外山宏行
A
デジタルドリルは、(アプリもよって機能は様々ですが)間違えたらすぐに正誤判定・解答解説が表示される、繰り返し何度も取り組めるなどのメリットがあります。また、自動採点による先生の負担軽減にもなります。プリントや紙のドリルと違って、全員が同じように指定された範囲をするだけでなく、補充的・発展的に活用することで、個別の学習支援が行いやすくなります。
しかし、紙の問題集やプリント同様、やらせっぱなしになると効果は薄いです。どんな問題が出題されるかを先生が把握しておくことが大事です。デジタルドリルに収録されている問題数には限りがありますので、十分な演習量を確保するには決してそれだけで十分とは言えない単元もあります。そして、学習履歴が見れるものならば、どの問題を間違えたかを個人と学級全体でつかみ、指導にいかしていくことがより効果的です。
近畿大学附属小学校 教諭 外山宏行
Q
自分はICTが苦手なのですが、毎時間使う必要はありますか?
2023.1.31 / 授業の進め方
回答者:近畿大学附属小学校 教諭 外山宏行
A
無理やり使う必要はありません。必要ならば使うという感じで構いません。しかし、令和3年3月版「学習指導要領の趣旨の実現に向けた 個別最適な学びと協働的な学びの一体的な充実に関する 参考資料」の中でも、「児童生徒自身がICTを「文房具」として自由な発想で活用できるよう環境を整え、授業をデザインすることが求められます。」とあります。
ICTの活用は算数科の中だけでなく、学校生活全般にわたることであり、文房具のように自由な発想で活用できるようにするためには、それぞれの教科学習の中で活用を進める必要があります。そのためには、指導者がある程度できること・できないことを理解し、子供たちに活用できる機会を提供しなければいけません。
今はインターネット上でもたくさんの実践や活用事例を見ることができ、気軽に参加できる無料のオンラインでの実践発表やワークショップなども多数あります。まずは情報を集めるところから始めたらよいと思います。
近畿大学附属小学校 教諭 外山宏行
Q
子供が授業中に情報端末で遊んだり余計なことをしたりするのではないか心配です。
2023.1.31 / 授業の進め方
回答者:近畿大学附属小学校 教諭 外山宏行
A
あることだと思います。それは、情報端末のあるなしに関わらず、子供が学びに向かえていない合図でもあります。すべてを子供のせいにするわけにはいきません。本当に子供が集中できるような課題になっているか、授業を受けているクラスの雰囲気はどうかなど、授業デザインを見直して、指導者自身の問題として改善していく必要があります。
また、活用度の低い授業や学級ほど、子供が遊んでしまう傾向があるように思います。情報端末を使う機会が少ないほど、使う機会に色々とやってみたくなるものです。普段から活用を進め、何かあった時々にその問題を共有して話し合っていくことが大切です。
近畿大学附属小学校 教諭 外山宏行
Q
「主体的に学習に取り組む態度」は、どのように評価すればよいのですか。
2022.12.23 / 資質・能力、授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
子どもに育成すべき資質・能力の三本柱の一つに「学びに向かう力、人間性等」があります。このうち、観点別評価できる部分が「主体的に学習に取り組む態度」です。したがって、他の二つの観点と同じように、子どもの学習のようすを分析的に捉えて評価しなければいけません。その方法は、次の2つです。
- ●先生による評価
授業中の発言や行動、ノートの記述等が評価の対象になります。ただ、先生がすべてに目を通すことはできませんので、評価する場面を絞りましょう。例えば、「新しい知識や技能を身に付ける」、「試行錯誤して考える」、「自分の考えを他者に伝える」などの場面です。主体的に学習に取り組んだことが、これらの場面に結びついているかどうかが大切です。
- ●子どもの自己評価
前頁で述べたように、子ども一人ひとりが自分の学習を自己調整した結果を自己評価することができます。「まとめ」として子どもが記述しておけば、評価の貴重な資料になります。
元帝塚山大学 教授 勝美芳雄
Q
単元の順番はなぜ教科書によって違うのですか?
2022.12.23 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
単元の順番を決める最も重要な要因は、内容の系統です。算数は、系統性の強い教科ですので、かなりの部分はこれによって決まります。例えば、計算は、たし算→ひき算→かけ算→わり算の順に指導しなければ子どもの学習がうまくいかないことは、よくおわかりでしょう。
しかし、例えば、「数と計算」の単元と「図形」の単元をどのような順番にするかは、多くの場合、内容の系統では決まりません。そのような場合は、学習の時期や子どもの学習の負担などを考えて順番を決めるので、教科書の作成者が、どんな子どもや学校を想定するかによって違いがでてくるのです。
さらに重要なのは、単元の順番を決めることは、年間指導計画をつくることであり、ひいては教育課程(カリキュラム)の編成につながります。教育課程を編成るのは各学校ですから、主たる教材である教科書を踏まえつつ、場合によっては、学校や地域の実情に合わせて単元の順番を各学校で変更することもあるのです。
元帝塚山大学 教授 勝美芳雄
Q
等分除と包含除は何が違うのですか?
2022.09.06 / 数学的な見方・考え方
回答者:元帝塚山大学 教授 勝美芳雄
A
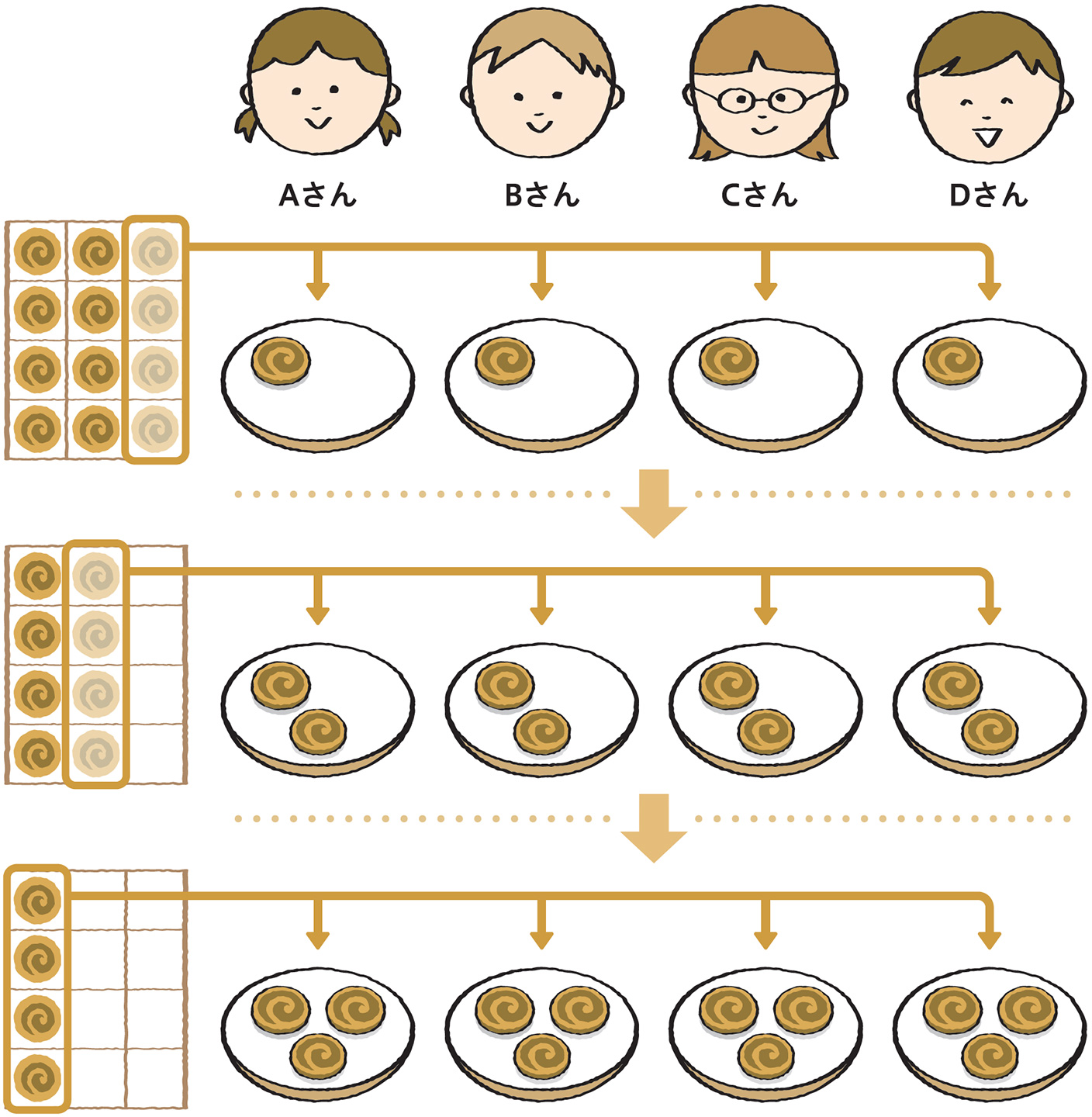
3年生で初めて学習する除法に等分除と包含除があります。3年生に指導する用語としては難しすぎますので、教科書などでは、等分除を「1人分をもとめる計算」、包含除を「何人分をもとめる計算」のように表現しています。実際の学習では、子どもたちは、例えば次のような、より具体的で代表的な場面をとおして理解します。
- 等分除…12このおかしを、4人で同じ数ずつ分けます。1人分は何こになリますか。
- 包含除…12このおかしを、1人に4こずつ分けます。何人にわけられますか。
さらには、次のような図によって、等分除と包含除の場面は同じ操作と見ることができます。このことから、違う場面を同じ除法で表せるということを理解することも必要です。
元帝塚山大学 教授 勝美芳雄
Q
教科書はどのタイミングで見せればいいですか?
2022.04.28 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
「算数授業のススメ」のVOL.1で解説した問題解決型学習の授業を想定すると、それぞれの段階で以下のように考えられます。
- ①「課題提示」の段階で見せる。……教科書の問題を使って展開し「めあて」を設定します。
- ②「自力解決」の段階で見せる。……自力解決が進みにくいときのヒントにします。
- ③「集団解決(練り上げ)」の段階で見せる。……集団解決が進みにくくなったとき、いろいろな考えを比較検討する参考にします。
- ④「まとめ」の段階で見せる。……教科書を参考にして、本時のまとめをします。
①と④は、どちらか一方、もしくは両方で見せることが考えられます。②と③は、子どもや学級の実態に応じて、見せるかどうかを選択しましょう。
元帝塚山大学 教授 勝美芳雄
Q
たし算の筆算の学習のとき、繰り上がりの「1」はどこにかくように指導するといいですか?
2022.04.28 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
たし算の筆算の繰り上がりの「1」は、計算間違いを防ぐために補助的にかくものです。一般的には、下のようなかき方があり、教科書でもいずれかを記載しています。
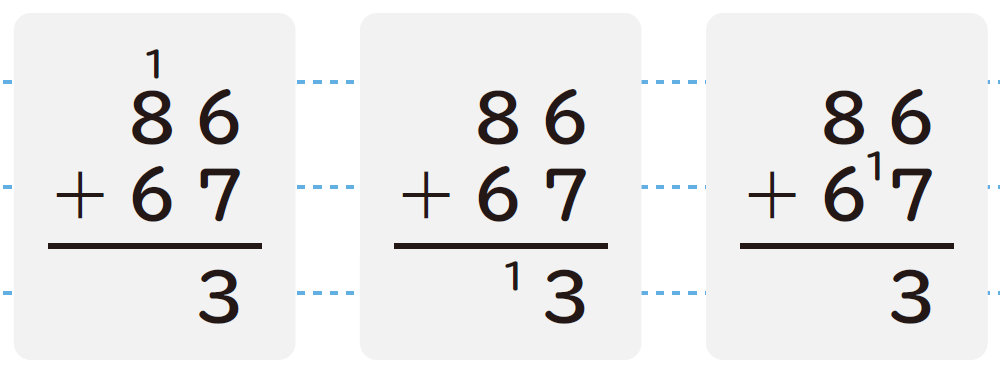
使っている教科書のかき方で指導してもよいですが、統一して決められたかき方はないので、子どもが計算しやすい方法でかくように指導しましょう。その際、自分がかく場所を決めた理由を説明できれば、なおよいです。また、計算に習熟して、この補助的な記載が必要なくなれば評価に値するでしょう。
なお、先生方は、筆算のかき方自体が万国共通で決められたものではないことを知っておくようにしましょう。
元帝塚山大学 教授 勝美芳雄
Q
子どもに身近な素材の問題にしたいとき、問題の数値は変えてもいいですか?
2022.01.07 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
算数の授業において、取り上げる問題の数値は極めて重要な要素の一つです。
数値を検討する視点の一つとして、「取り上げる数値が子どもの実態に合っているか」が重要です。したがって、質問にある「子どもの身近な素材」の数値になっているかを考え、場合によって数値を変更することはあり得ます。
ただし、「子どもの身近な素材」にしたために、授業の目的の達成に支障がきたされないようにしましょう。たとえば、数値が簡単すぎて解決すべき課題が出てこなくなったり、逆に、数値が複雑すぎたり大きすぎたりして問題解決が進まないことになったりしてはいけません。
元帝塚山大学 教授 勝美芳雄
Q
計算問題は得意なのに文章題は苦手な子どもには、どのように指導すればいいですか?
2022.01.07 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
このような子どもは、文章題で示される場面が理解しにくいことが多いでしょう。その理由は、算数の文章題が不要な要素を省いた簡潔な表現であることや、算数独特のいい回しなどが挙げられます。
そこで、文章題が示す場面を、わかりやすく変えるさまざまな表現方法が、算数教育の歴史の中で開発されてきました。たとえば、具体的な絵、数量の関係を表す図(テーブ図、線分図、面積図など) 、ことばの式などで、これらは教科書にも示されています。
文章題が苦手な子どもには、まず、これらの方法を用いて指導し、子ども一人ひとりが自分にとってわかりやすい方法を獲得することを目指しましょう。このとき、先生の「おすすめ」の方法はあっても構いませんが、「おしつけ」になっては子どもの力はつかないので注意が必要です。
元帝塚山大学 教授 勝美芳雄
Q
集団解決のときの子どもの考えの取り上げ方を教えてください。
2021.09.07 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
取り上げる子どもの考えは、まず授業計画の際に予想しておきます。そして授業では、子どもの自力解決を個別支援する際に、個々の考えを把握しながら、取り上げる考えとその順番を考えます。学習がスムーズに進むよう、最初に本時の目標となる典型的な考えを取り上げ、その後、個性的な考えや発展的な考えを取り上げるようにします。
注意すべきは、子どもがつまずきやすい誤りの取り上げ方です。自力解決の際にこのような考え方をしている子どもがいれば、正しい考え方に修正できるよう支援し、集団解決で修正の過程を発表させましょう。誤りのみを発表させ、学習意欲を失わせることがないようにしましょう。
元帝塚山大学 教授 勝美芳雄
Q
教科書の練習問題は全部取り組ませないといけませんか?
2021.09.07 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
教科書の練習問題には、1時間の授業の最後に取り組む「練習問題」と、単元末や学年末に取り組む「まとめの問題」があります。
問題解決型学習のまとめの段階では、その時間に学んだことが一般的に成り立つことを「練習問題」で確認します。確認のためには子どもによる解答の発表も必要なので、全部に取り組む時間がないこともあるでしょう。その場合は、あらかじめ選んでおいた典型的な問題に取り組ませ、残りは家庭学習にしてもよいでしょう。
「まとめの問題」は1時間で取り組める分量が設定されているので、原則すべてに取り組ませ、時間が足りない子どもには個別に補充の指導をしましょう。
元帝塚山大学 教授 勝美芳雄
Q
教科書は授業中ずっと開いていないといけませんか?
2021.06.18 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
教科書には、各単元の授業で考える問題についての考え方、解決の結果、そして、問題解決から導き出す結論などが記載されています。したがって、子どもが授業中ずっと教科書を開いている必要は、ありません。授業の最初に問題場面を把握したり、逆に、授業の最後に内容をふり返って結論をまとめたりするときに開くことが多いでしょう。また、既習事項をふり返る際には、当該の単元以外の部分を開くこともあるでしょう。
元帝塚山大学 教授 勝美芳雄
Q
一部の子どもの考えだけで授業が進んでしまうときはどうすればいいですか?
2021.06.18 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
「〇〇さんの考えがわかりましたか?」とか、「〇〇さんの考えをもう一度言ってみましょう。」など、先生が他の子どもに確認したり問い返したりすればよい、とよく言われます。これでうまくいけばいいのですが、他の子どもがあまり反応しないことも多いようです。
そこで、先に発言したい子どもには先生だけに考えを伝えさせ、先生は「なるほど、よく考えたね。」などと反応した後、他の子どもに「〇〇さんは、なんと言ったと思う?」と聞いてみてはどうでしょう。他の子どもがわかりにくそうにしている時は、先生が部分的に伝えるなどすれば、みんなで考えることができるでしょう。
元帝塚山大学 教授 勝美芳雄
Q
既習事項のふり返りでは、子どもたちに何を意識させればいいですか?
2021.06.18 / 授業の進め方
回答者:元帝塚山大学 教授 勝美芳雄
A
既習事項をふり返る目的は、問題解決の見通しをもつためです。したがって、子どもたちに意識させたいのは、既習事項と当該授業の問題の比較です。既習事項と当該授業の問題に共通点が多い場合は、既習事項を使って問題を解決するという見通しがもてます。逆に、既習事項と当該授業の問題にちがいが多い場合は、発想を変えて新しい解決方法を考え出すことが必要になります。
元帝塚山大学 教授 勝美芳雄
Q
これまでの学習指導要領で示されていた「数量関係」領域の内容は、どのように取り扱われますか。
2019.05.29 / 学習指導要領
回答者:日本文教出版 編集部
A
従前の「数量関係」領域では、主として、関数の考え、式の表現と読み、及び資料の整理と読みの3つの下位領域からなるものでした。
今回の改訂により、それぞれの内容は、次のように取り扱われることになりました。
「式の表現と読み」に関する内容は、数と計算の考察に必要な式として捉え直され、「A数と計算」領域に位置付けられました。これにより、事象を考察する際の式の役割が一層理解しやすくなり、日常生活の場面や算数の学習の場面で、式に表現したり読んだりして問題解決することができるようになります。
「関数の考え」に関する内容は、4年以降に設けられた「C変化の関係」領域に位置付けられました。しかしながら、1~3年でも、数や図形などの考察において、数の関係を考察したり、変化の規則に注目したりする場面が多いことに注意が必要であり、そのような場面は「関数の考え」の素地指導をする重要な機会となります。
「資料の整理と読み」に関する内容は、統計的な内容の充実を踏まえ、「Dデータの活用」領域に位置付けられました。身の回りの事象をデータから捉え、問題解決に生かす力、データを多面的に把握し、事象を批判的に考察する力の育成を目指すことが大切です。
日本文教出版 編集部
Q
算数では、プログラミング教育について、どのように配慮すればよいですか。
2019.05.29 / 学習指導要領、資質・能力
回答者:日本文教出版 編集部
A
小学校学習指導要領の総則に、プログラミングを体験しながらコンピュータに意図した処理を行わせるために必要な論理的思考力を身に付けるための学習活動を、計画的に実施することが明記されました。
算数では、「第3 指導計画の作成と内容の取扱い」2(2)で、「(前略)プログラミングを体験しながら論理的思考力を身に付けるための活動を行う場合には、児童の負担に配慮しつつ、例えば第2の各学年の内容の〔第5学年〕の「B図形」の(1)における正多角形の作図を行う学習に関連して、正確な繰り返し作業を行う必要があり、更に一部を変えることでいろいろな正多角形を同様に考えることができる場面などで取り扱うこと。」と、プログラミングを行う学習場面が例示されました。
小学校におけるプログラミング教育のねらいは、「プログラミング的思考」を育むことにあります。「プログラミング的思考」とは、自分が意図する一連の活動を実現するために、どのような動きの組み合わせが必要か、どのように改善していけばより意図した活動に近づくのかということを論理的に考えていく力です。
ここで注意して欲しいのは、算数で大切なことは、「プログラミングを教えること」ではなく、「プログラミング的思考を育むこと」だという点です。
「プログラミング的思考」は、プログラミング以外の算数の学習活動でも身に付けられます。例えば、位ごとに数の大きさを比べることをくり返し大きな数の大小を調べる活動や、筆算のしかたや仕組みを順序立てて考える活動は、プログラミング的思考の育成が期待できる学習内容だと考えられます。
日本文教出版 編集部
Q
算数における評価は、どのように考えればよいですか。
2019.05.29 / 学習指導要領
回答者:日本文教出版 編集部
A
児童の学習評価や指導要録等の改訂に関する資料は、以下の文部科学省のサイトから確認できます。
http://www.mext.go.jp/b_menu/hakusho/nc/1415169.htm![]()
また、算数・数学に関する資料は、以下の文部科学省のサイトの[別紙4]P.6-9に掲載されています。
http://www.mext.go.jp/b_menu/hakusho/nc/attach/1415195.htm![]()
日本文教出版 編集部
Q
各学年の目標は、どのように設定されていますか。
2019.02.19 / 学習指導要領、資質・能力
回答者:日本文教出版 編集部
A
学年の目標は、一般的かつ包括的に示された算数科の目標を実際の学習指導で達成させるために、算数の内容の系統性と児童の発達段階に応じて、学年ごとに具体的に示されています。そして、算数科の目標と同様に、各学年で育成を目指す資質・能力の三つの柱である「知識及び技能」、「思考力、判断力、表現力等」、「学びに向かう力、人間性等」に沿ってそれぞれを(1)、(2)、(3)としています。なお、(1)、(2)については、各学年で指導すべき主な内容と対応しています。
また今回の改訂では、児童の発達の段階に応じて、第1学年、第2学年と第3学年、第4学年と第5学年、第6学年の4つの段階を意識した記述となっています。
日本文教出版 編集部
Q
数学的活動は、学習指導要領にどのように位置付けられていますか。
2019.02.19 / 学習指導要領、数学的活動
回答者:日本文教出版 編集部
A
数学的活動は、5つの領域の指導内容からいったん切り離した上で、3つもしくは4つの活動に集約して、算数科の各学年の内容に位置付けられています。
その際、数学的な問題発見、問題解決の過程に位置付く「日常の事象から見いだした問題を解決する活動」、「算数の学習場面から見いだした問題を解決する活動」及び「数学的に表現し伝え合う活動」という観点から整理されています。なお、第1~3学年については、身の回りの事象を観察したり、小学校に固有の具体的な操作をしたりすること等を通して、数量や図形を見いだして、それらに進んで関わって行く活動が位置付けられており、小学校における学習に特徴的な数学的活動を重視することとされています。
また、児童の発達段階を踏まえ、算数科と数学科の接続の視点から、第1学年、第2学年と第3学年、第4学年と第5学年、第6学年の四つの段階を設定し、数学的活動が示されています。
日本文教出版 編集部
Q
新設された「データの活用」領域の扱いで配慮すべきことはありますか。
2019.02.19 / 学習指導要領
回答者:日本文教出版 編集部
A
今回の学習指導要領改訂で、統計的な内容が充実されたことをふまえ、身の回りの事象をデータから捉え、問題解決に生かす力、データを多面的に把握し、事象を批判的に考察する力の育成を目指すとともに、小学校と中学校間との統計教育の円滑な接続を図るため、これまでの「数量関係」領域の資料の整理と読みの内容を中心に、統計に関わる領域「データの活用」が新たに設けられました。
この領域では、目的に応じてデータを収集、分類整理し、結果を表やグラフ等に適切に表現するための知識・技能の習得に加え、「問題-計画-データ-分析-結論」というような段階からなる統計的な探究プロセスについて知ること、データのもつ特徴や傾向を把握し、問題に対して自分なりの結論を出したり、その結論の妥当性について批判的に考察したりすること、統計的な問題解決のよさに気付き、データやその分析結果を生活や学習に活用しようとする態度を身に付けることについても、児童の発達段階をふまえて意識することが大切です。
日本文教出版 編集部
Q
小学校算数科の学習指導要領改訂の要点を教えて下さい。
2018.11.26 / 学習指導要領
回答者:日本文教出版 編集部
A
主に次の5点が考えられます。
- ①算数科で育成を目指す資質・能力を明確にするために、目標及び内容が資質・能力の3つの柱で整理されました。
- ②算数科で目指す資質・能力を育成する観点から、数学的活動の一層の充実が求められました。
- ③数学的活動を通して働かせる数学的な見方・考え方や、育成する資質・能力に基づき、領域の構成が見直されました。
- ④複数のグループの比較を可能とするなど、統計に関する内容が充実されました。
- ⑤簡単な割合を用いた比較の仕方を新たに取り扱うなど、全国学力・学習状況調査などで課題として挙げられていた割合に関する内容が充実されました。
日本文教出版 編集部
Q
小学校算数科で育成する資質・能力とはどのようなものですか。
2018.11.26 / 学習指導要領、資質・能力
回答者:日本文教出版 編集部
A
今回の学習指導要領の改訂では、育成を目指す資質・能力を「(1)知識及び技能」、「(2)思考力、判断力、表現力等」「(3)学びに向かう力、人間性等」の三つの柱に沿って明確化することが求められています。
算数科の目標についても、以下の通り三つの柱によって整理して示され、上記の(1)~(3)に、それぞれ対応しています。
数学的な見方・考え方を働かせ、数学的活動を通して、数学的に考える資質・能力を次のとおり育成することを目指す。
- (1)数量や図形などについての基礎的・基本的な概念や性質などを理解するとともに、日常の事象を数理的に処理する技能を身に付けるようにする。
- (2)日常の事象を数理的に捉え見通しをもち筋道を立てて考察する力、基礎的・基本的な数量や図形の性質などを見いだし統合的・発展的に考察する力、数学的な表現を用いて事象を簡潔・明瞭・的確に表したり目的に応じて柔軟に表したりする力を養う。
- (3)数学的活動の楽しさや数学のよさに気付き、学習を振り返ってよりよく問題解決する態度、算数で学んだことを生活や学習に活用する態度を養う。
日本文教出版 編集部
Q
「数学的な見方・考え方」とはどのようなものですか。
2018.11.26 / 学習指導要領、数学的な見方・考え方
回答者:日本文教出版 編集部
A
今回の学習指導要領の改訂では、児童が各教科等の特質に応じた物事を捉える視点や考え方(以下「見方・考え方」という)を働かせながら、資質・能力の育成を目指すことが目標として示されています。
学習指導要領解説では、{「数学的な見方」については「事象を数量や図形及びそれらの関係についての概念等に着目してその特徴や本質を捉えること」}、{「数学的な考え方」については「目的に応じて図、数、式、表、グラフ等を活用し、根拠を基に筋道を立てて考え、問題解決の過程を振り返るなどして既習の知識及び技能等を関連付けながら統合的・発展的に考えること」}であると考えられています。
これらのことをふまえ、算数科における「数学的な見方・考え方」は、「事象を、数量や図形及びそれらの関係などに着目して捉え、根拠を基に筋道を立てて考え、統合的・発展的に考えること」として示されています。
なお、「数学的な見方・考え方」は、これまで教科目標や評価の観点名として用いられてきました。しかし、今回、小学校算数科において育成を目指す資質・能力の三つの柱を明確化したことにより、どのような視点で物事を捉え、どのような考え方で思考をしていくのかという、算数の学習における物事の特徴や本質を捉える視点、思考の進め方や方向性を意味することになりました。
日本文教出版 編集部
Q
「算数的活動」が「数学的活動」に変わりましたが、両者に違いはありますか。
2018.11.26 / 学習指導要領、数学的活動
回答者:日本文教出版 編集部
A
平成10年告示の学習指導要領における算数科の目標において、用語「算数的活動」が初めて用いられました。平成20年告示の学習指導要領では、その意味が「児童が目的意識をもって主体的に取り組む算数にかかわりのある様々な活動」と規定されました。そして、基礎的・基本的な知識・技能を確実に身に付けるとともに、数学的な思考力・表現力を高めたり、算数を学ぶことの楽しさや意義を実感したりするために、重要な役割を果たすものと位置づけられました。また、小学校で算数的活動を生かした指導を一層充実させ、言語活動や体験活動を重視した指導が行われるようにするために、各学年の内容に算数的活動が具体的に示されました。
今回の学習指導要領改訂では、育成を目指す資質・能力の観点からの目標や内容の検討において、「数学的な見方・考え方」を働かせた学習を展開するよう内容を整理すること、また学習指導の過程においては、数学的な問題発見や問題解決の過程を重視することが求められています。そこで、数学的な問題発見や問題解決の過程における様々な局面と、そこで働かせる数学的な見方・考え方に焦点を当てて児童の活動を充実させるために、用語「算数的活動」を「数学的活動」と改めて、その趣旨を一層徹底させることになりました。
日本文教出版 編集部
Q
領域の構成はどのように変わりましたか。
2018.11.26 / 学習指導要領
回答者:日本文教出版 編集部
A
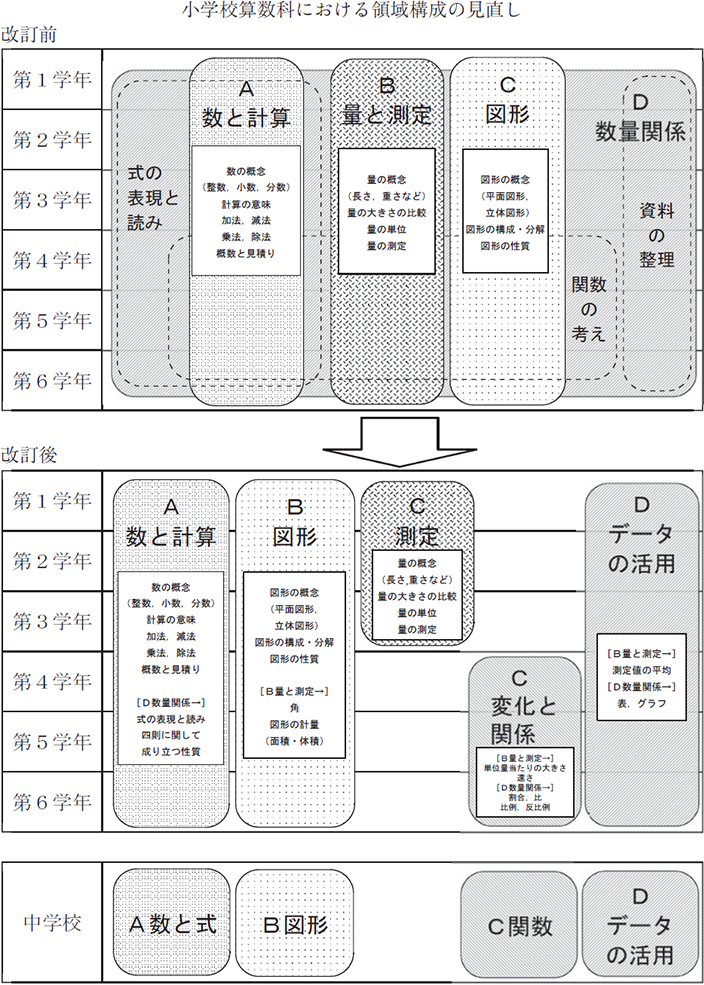
算数科の内容は、「A 数と計算」、「B 図形」、「C 測定」(下学年)、「C 変化と関係」(上学年)、及び「D データの活用」の五つの領域で示されています。これは、小学校における主要な学習の対象、すなわち、数・量・図形に関する内容とそれらの考察の方法を基本とする領域(「A 数と計算」、「B 図形」、「C 測定」)、さらに事象の変化や数量の関係の把握と問題解決への利用を含む領域(「C 変化と関係」)、不確実な事象の考察とそこで用いられる考え方や手法などを含む領域(「D データの活用」)を、それぞれ設定したものになっています。
変更された点は次の通りです。
- ①「A 数と計算」の充実:「式の表現や読み」のA領域への位置付け
従前は「数量関係」において、第1学年から第6学年まで位置付けられていた式の表現と読みに関する内容を、「数と計算」の考察に必要な式として捉え直し、「A 数と計算」領域に位置付け直しました。 - ②量を測定するプロセスの充実(下学年)と図形の計量的考察の充実(上学年)
従前の「B 量と測定」の内容を、測定のプロセスを充実する下学年での「C 測定(下学年)」領域と、計量的考察を含む図形領域としての上学年の「B 図形」に再編成しました。再編成に当たっては、まず、新規に「C 測定(下学年)」領域を設定することにしました。次に、基本的な平面図形の面積や立体図形の体積などの学習を、図形の特徴を計量的に捉えて考察するという視点から位置付けし直し、上学年における「図形」領域の内容に移行しました。最後に、単位量当たりの大きさや速さについては、二つの数量の関係について考察することを重視する観点から、「変化と関係」領域で扱うことにしました。 - ③変化や関係を把握する力の育成の重点化と統計教育の充実:数量関係領域の充実
従前の「数量関係」は、主として<関数の考え><式の表現と読み>及び<資料の整理と読み>の三つの下位領域からなるものでしたが、今回の改訂により、従前の「数量関係」の内容を新たに設けた「変化と関係」と「データの活用」に移行しました。
日本文教出版 編集部
Q
学習指導要領改訂に伴う移行措置はどのようになっていますか。
2018.11.26 / 学習指導要領、移行措置
回答者:日本文教出版 編集部
A
算数科については、次のように新課程の内容を前倒ししたり省略したりすることにより、新課程に円滑に移行できるようにします。
(○印は追加、●印は削除)
【2018年度】
| 学 年 | 内 容 |
|---|---|
| 第3学年 |
|
| 第4学年 |
|
【2019年度】
| 学 年 | 内 容 |
|---|---|
| 第3学年 |
|
| 第4学年 |
|
| 第5学年 |
|
なお、2019年度の移行措置内容のうち、第4学年「小数倍」「簡単な場合の割合」、第5学年「速さ」については、文部科学省より補助教材が供給される予定です。
日本文教出版 編集部