 |

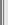 |
教育実践例 |
 |
|
 |
 |
イチローの年間安打数を予測する
−モデル化とシミュレーションの授業− |
|
| |
|
| 1.はじめに |
今年,アメリカ大リーグでは,日本からやってきた一人のバッターが,1920年にG・シスラーによってつくられた年間最多安打数257本の大記録に挑戦している。「している」と現在形で書いたのは,この一文を読まれている方にとっては過去のことでも,この原稿を書いている9月の私には楽しみな未来の1つだからだ。
80数年前の過去と,記録が破られるかもしれない近い未来。その間に身を置いている人間は,記録の可能性を期待を込めて予測しようとする。カウントダウンに入ってからマスメディアは連日,「あと一試合平均○○本打てば最多に並ぶ!」といったコメントを我々に届けている。ところが当のイチローは,ノーヒットの試合でダメかもしれないと思わせた次の日,ほとんど起こらないはずの1試合5本のヒットを量産して,ファンを一喜一憂させているのだ。
この平均と変動こそが,シミュレーションのおもしろさの1つだろう。
ここでは,情報Bの授業で行なったモデル化とシミュレーションの授業の題材として,イチローを取り上げた授業実践例を紹介しようと思う。 |
|
|
 |
| 2.イチローのデータを取得 |
さて,イチローの日々の記録は,イチローの古巣ブルーウェイブのサイト(http://www.bluewave.nu/ichiro51/index.html)に掲載されている。彼が日本にいるときの記録も,大リーグに行ってからの記録も,彼のプレーの後にぴったりとついて更新され続けている。授業は,このデータを使ってパソコンの中にイチローを再現する。そして,残り試合の仮想の打席にイチローを立たせ,戦わせ,年間の安打数や最終打率を予想しようというものである。
まず,このサイトにアクセスし,現在までの全打席のデータを取得する。
このレポートでは7月31日までのデータを取得し,その後のイチローを予測することにする。データはコピー&ペーストで,簡単にエクセルなどのシートに貼り付けることができる。
次に各試合の打席数と安打数だけにデータをしぼったシートを別につくる。そして並べ替えを行ない,ノーヒットに終った試合数から,5本のヒットを打った試合数まで安打数ごとに数え上げる。
まずはこうやって,イチローが7月31日現在で1試合あたり何本の安打を打っているかをグラフ化したものが図Ⅰである。イチローの1打席1打席の真剣勝負から,このような美しい分布が生まれてくることに不思議な感慨を抱くのは私だけだろうか。
▲図Ⅰ イチローの1試合あたりの安打数(4月6日〜7月31日) |
|
|
 |
| 3.ICHIROサイコロをつくる |
(1)相対度数の算出
次に,このデータをもとにイチローが1試合で打つ安打数の相対度数(確率)を計算する。8月以降の成績を予測するには,この相対度数に従って安打の出るICHIROサイコロをパソコンの中につくる必要がある。このICHIROサイコロを未来の1試合ごとに振って,何安打打ったかをシミュレーションするのである。仮想イチローのバッターボックスでの戦いは,気が抜けるほど汗をかかないあっさりしたものになる。
相対度数の計算は簡単だ。7月31日まででイチローの出場した試合数は101試合。例えば安打3を打った試合は14試合あるから,14÷101で相対度数(確率)は0.139となる。こうやって計算してみると,7月末の段階で,その試合がノーヒットに終る相対度数は0.178,安打1本の相対度数は0.337,打2本の相対度数は0.307といった具合になる。安打4本の試合となると0.030。そして安打が5本出る相対度数は0.010。確率は1%しかない。実はイチローが1試合5本の安打を打ったのは7月29日のエンジェルス戦が最初である。7月31日の時点では,1試合5本のヒットというのは1回しか実現していなかったのである。
(2)累積相対度数のアイデア
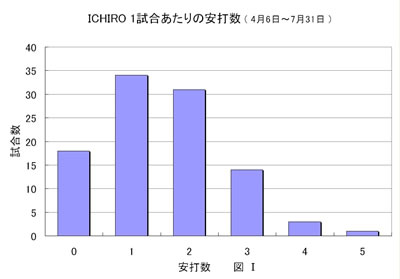
この相対度数を使ってICHIROサイコロをつくるには,累積相対度数というアイデアを使う。
試合ごとに0〜1までの一様乱数を発生させ,その値が0.178以下だったらその試合はノーヒットということにする。発生した乱数が0.178より大きくて0.178に0.337を加えた0.515以下だったらヒットが1本出たとする。2本目から5本目まで同様に各相対度数を加えた(累積した)値を境界とし安打数を出していく。つまり,0〜1までの一様な乱数の分布の中に安打数の境界線を引くことになる。
図Ⅱは,イチローの安打数の累積相対度数グラフである。0〜1までの乱数をパソコンに1個発生させ,その値が0.75だったとすると,グラフからその試合の安打数は2本だったことになる。
▲図Ⅱ イチローの安打累積相対度数
(3)累積相対度数の理解
累積相対度数の考え方がこの授業の最も大事なところだが,生徒たちにいきなりこの累積相対度数の考えを示すのは難しい。したがって,前もってランダムウォークモデルといわれる簡単なシミュレーションとその応用を学習させている。
ランダムウォークモデルのつり銭問題はよく知られている。
例えば,文化祭でバザーを行なうことにしたクラスがあるとする。中古のCDや漫画の単行本を持ち寄り,すべて150円で販売することにした。商品は100点集まった。さて,つり銭の50円玉を何枚準備しておけば大丈夫かという問題である。50円のおつりが必要な客とそうでない客はちょうど半々になると仮定しておく。つまり相対度数はおのおの0.5ということになる。また,客1人につき1品しか買わないとする。
このとき,客ごとに0〜1までの一様乱数を発生させる。乱数が0.5以下だったらその客は150円出した客でつり銭は必要ない。0.5より大きかったら200円出した客で,50円のつり銭が必要だとする。この50円玉の収支を100回(客100人分)行なって50円玉の不足分を割り出す。これを文化祭50年分ほどやれば,50円玉の不足分合計が変動するグラフをつくることができる。ここから生徒たちは,50円玉を何枚程度用意しておけば80〜90%程度の信頼度でつり銭の準備は大丈夫かを見つけ出すことができる。
さて,このシミュレーションのあとにこんな課題を与える。
「それでは10人に1人の確率で,500円玉を出すような客がくると想定した場合,つり銭の50円玉と100円玉は何枚準備しておけばよいでしょう。
このとき,今度は0〜1までの一様乱数分布の真中の0.5で線引きするのではなく,0.45と0.90で線引きすることを学習させるのである。例えばエクセルのセルに入れる計算式は次のようになる。
=IF(RAND()<0.45,200,IF(RAND()<0.90,150,500))・・・① |
|
|
 |
| 4.仮想イチローの戦い |
(1)打席に立つ準備運動
累積相対度数の理解ができたら,いよいよ表計算のシートに残り試合のシミュレーションを行なっていく。160試合まですべてイチローは打席に立ったとして,仮想イチローには,残り59試合を戦ってもらう。乱数によって安打数を決定するセルの計算式はずいぶん長ったらしくなるが,生徒たちは頭をひねって考えてくれる。要は計算式①の応用である。
試合ごとの打席数はどうすればいいだろう。生徒から質問が出る。試合ごとの打席数の変動もシミュレーションすることが可能だが,複雑になるので,ここではそれまでの打席数を単純に貼り付けることにする。
かくしてICHIROサイコロは生徒たちの表計算シート上で動き出すことになる。
(2)100回のシミュレーション
7月いっぱいまでのデータを使ってICHIROサイコロをつくり,シミュレーションした結果は,1回について1つの結果しか出てこない。例えば年間252本の安打数になって,最終打率は3割5分6厘といった具合だ。
そこで,100回のシミュレーションを生徒たちに指示する。都合のいいことにエクセルの乱数は再計算ごとに値を変えてくれる。したがって,100回のシミュレーションの結果をセルに書き込むことはあまり時間がかからないのだ。生徒たちにとって,この100回シミュレーションの意味は即座には理解しがたい。生徒たちは平均という考え方はよく分かっているが,そこからのばらつき,変動といった考えになじんでいるものは少ない。
(3)仮想イチローⅠ号の結果
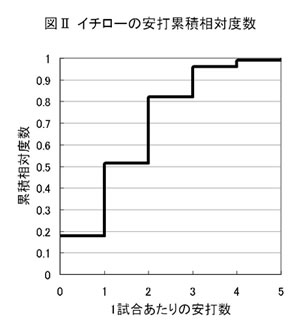
この100回のシミュレーションの年間安打数の結果をグラフにしたのが図Ⅲである。
▲図Ⅲ ICHIROサイコロによる大リーグ年間安打数予測(仮想イチローⅠ号の場合)
この結果から,すぐ気づくことがある。とても257本まで行かないじゃないか!そうなのである。4,5,6,7月という4ヶ月を平均した成績では,257本の記録を抜けないのである。せいぜい打っても249本。それも100回の試行で1回程度の出現率だから,確率は1%程度である。
仮想イチローⅠ号のモデルの最大の欠点は,4ヶ月の平均化モデルだということである。尻上がりに調子を上げてきたイチローを再現するにはこの平均化モデル「仮想イチローⅠ号」では無理なのである。
(4)仮想イチローⅡ号の登場
それでは月間51本を打った7月の調子がその後も続くと仮定したらどうだろう。つまり,7月の調子がそのまま出るICHIROサイコロをつくってみることにする。
7月の成績だけをグラフ化したものが図Ⅳである。そして,その累積確率から年間安打数をシミュレーションしたものが図Ⅴになっている。
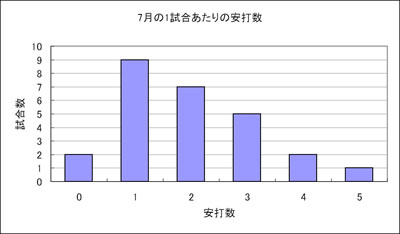
▲図Ⅳ イチローの7月の1試合あたりの安打数
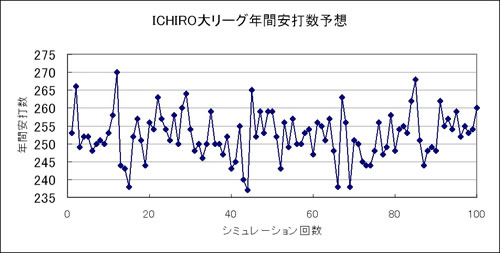
▲図Ⅴ ICHIROサイコロによる大リーグ年間安打数予測(仮想イチローⅡ号の場合)
すると100回の試行で24回は257本に並ぶかそれ以上という結果になる。逆説的だが,イチローの年間最多安打の可能性が出てきたのは,7月の爆発的な調子がそれ以降も続いたということに尽きる。6月までは予測さえできなかったのである。
アメリカと日本の野球文化の微妙な違いで,アメリカは年間安打200本以上を打ち続けるイチローを高く評価するが,日本は平均打率の意識が高く,首位打者の評価が高い。打率は分母が小さくてもなりたつが,最多安打はいかに多く打席に立つかということも必要になる。イチローが日本にいる頃から年間200本安打にこだわってきたのも,目標とするプレーヤーが大リーグにいるのも今分かるような気がする。 |
|
|
 |
| 5.イチローと生徒たち |
この授業は,本校の文科総合科の1年生を対象に行なったものである。ただ,実際に生徒たちがやったシミュレーションは,6月いっぱいまでの結果を使っている。彼らが学習した7月上旬は,イチローの最多安打の話は巷にはなく,首位打者になれるか!?という視点でシミュレーションが行なわれた。
授業形態も一般的な例からする少し特殊かもしれない。本校では2学期制をとっており,文科総合科という普通科系の専門学科は,前期に4単位を使って情報Bを実施し終了してしまう。生徒のレベルはある程度高く,まとまったテーマに集中しやすい単位数と環境であったことを断わっておかなければならない。
モデル化とシミュレーションの分野は,パソコンを道具に,思ってもいないテーマについて考えさせるので生徒たちの評判はよい。レポートの感想の欄には,「こんなことがパソコンを使ってできるのか」という驚きの声が数多く書かれてあった。 |
|
|
|
 |
 |
 |