小学校 算数
小学校 算数
※本実践は平成20年度版学習指導要領に基づく実践です。
1.単元名
「重なる形と図形の角を調べよう」 図形の角と合同
2.本時の位置づけ
第11時(全15時間)
3.本時のねらい
本時は、どんな四角形も一つの頂点から向かい合う頂点に向かってのばした直線(対角線)で2つの三角形に分けることができ、180°×2で、四角形の内角の和が360°になることが理解できるようにすることをねらう。図形を三角形に分割してみる見方はその後の多角形の角の大きさの和を求める学習で活用される見方であり、全員の子どもに、確実に身につけさせたい。そこで、本時のしる、わかる段階はスモールステップで指導を行いエラーレスで学習を展開し、使いこなす段階で全員が交流に参加しながら考えさせ、知識を確実なものにしていく習得の授業スタイルで展開する。まず「しる段階」では、4つの角の大きさがわかっている長方形や正方形を提示し、内角の和が90×4で360°である事を確認した後、不定形の四角形を提示することで、課題意識を持たせ、めあてをつかませる。「わかる段階」では、4つの角を色分けし、切る、動かすという操作が可能な図形カードを用いて教師と一緒に四角形の内角の和の求める方法を話し合い、2つの三角形に分けて考える方法で三角形の内角の和が求められ、提示された四角形の角の大きさの和が360°といえる事を確認し、見通しを持たせる。さらに、別の四角形を提示し、どんな四角形でも2つの三角形に分割して考える方法で内角の和が360°であることを説明できるか問いかけ、多様な四角形の内角の和を、2つの三角形に分割する方法で求めさせる。「つかいこなす段階」では、どんな四角形でも内角の和が360°になることを確認した後、4つの三角形に分割した四角形を追事象として提示し、内角の和は180°×4で720°になる。この分け方では三角形の角の大きさの和は求められないのかという視点で交流させ、四角形の内角の和として必要な部分と必要ない部分をより明確にし、四角形の内角の和が360度であるという知識理解を強化できるようにする。
4.本時の評価規準
○知識・理解
どんな四角形も、対角線で2つの三角形に分けることができ、三角形の内角の和が180°であることを使って、180°×2で四角形の内角の和が360°であると求められることを理解している。
5.単元の指導計画
|
時 |
主な学習内容と活動(※主な算数的活動) |
スタイル |
|---|---|---|
|
1 |
○パズルで形を構成する活動や薄い紙に写して重ねる活動、身のまわりの合同な図形を見つける活動。 |
習得 |
|
2 |
○合同な図形で対応する頂点、辺、角を見つけ、合同な図形では対応する辺の長さや対応する角の大きさが等しいことを理解する。 |
習得 |
|
3 |
○台形、長方形、ひし形、平行四辺形を分割してできた三角形について合同の考え方を適応して調べ、合同な三角形を見つける。 |
習得 |
|
4 |
○合同な三角形のかき方を理解し、作図し、作図の仕方を説明することができる。 |
習得 |
|
6 |
○合同な四角形の作図をする。 |
習得・活用 |
|
8 |
○三角形や四角形が敷き詰められた模様を観察したり、三角形を敷き詰めたりする活動。 |
習得 |
|
9 |
○三角形の内角の和が180°であることを理解する。 |
習得 |
|
10 |
○三角形の内角の和が180°であることを使って未知の角の大きさを求める事ができる。 |
習得 |
|
11 |
○四角形の内角の和が360°であることを理解する。 |
習得 |
|
12 |
○多角形の用語、意味を理解し、多角形を三角形に分割して内角の和を求める。 |
活用 |
|
13 |
○三角形や四角形の角の大きさの和を使って未知の角の大きさを求める問題を解く。 |
活用 |
|
14 |
○いろいろな平面図形を敷き詰めて模様づくりをする。 |
活用 |
|
15 |
○練習問題をして,学習の定着を図る。 |
|
6.実践紹介
(1) 本時展開【習得の授業スタイル】
|
|
学習活動 |
具体的な手立て |
|---|---|---|
|
し |
1.長方形や正方形と不定形の四角形Aを比較して話し合い、めあてをつかむ。
・正方形は4つの角が90°。90°×4で360° |
○事実として4つの角度が分かっている四角形と角度が分からない四角形Aを提示し、どんな四角形も内角の和が360°であるといえるか問いかける。 |
|
四角形の4つの角の大きさの和が何度になるか調べて説明できるようになろう。 |
||
|
わ |
2.四角形の内角の和を調べる。
|
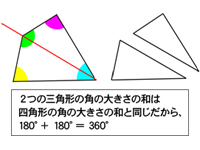
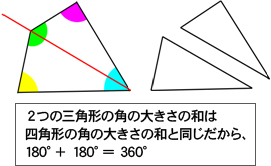
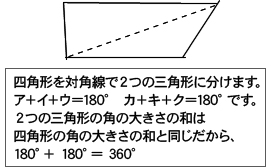
○2分割された四角形と分割前の四角形を並べて提示し、三角形の内角の和が180度であることを確認した後,これを使って四角形の内角の和が何度か求められないか問いかける。子どもと対話しながら四角形の角の大きさの和が2つの三角形の角の大きさの和と同じになることを図形カードを使っておさえ、代表児の説明を板書することで説明のモデルをつくる。 |
|
|
○掲示用のカードを分割し、角を寄せて提示し、360°になることを視覚的に確認する。 |
|
|
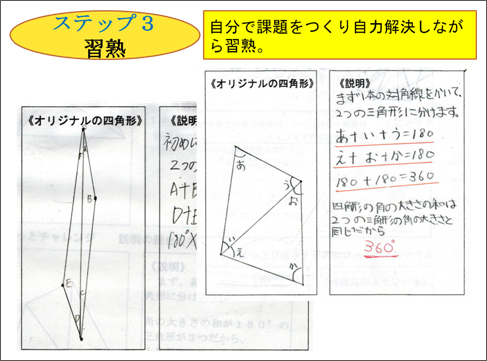
○自分で作った四角形を1本の対角線で分け角の大きさの和を調べる。
|
○どんな四角形でも角の大きさの和が360度であると説明できるか問いかけ、自分で四角形を作り、角の大きさの和を求めるよう指示する。 |
|
|
つ |
3.いろいろな四角形の角の大きさの和の求め方を話し合う。
|
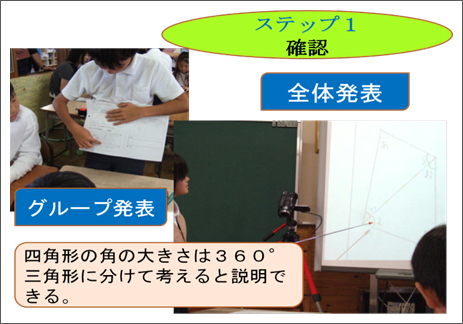
○グループで自分が調べた四角形を使って説明し合うよう指示し、グループで説明しあった後、代表児1名の四角形の説明をもとに、どんな四角形の内角の和も360°である事を押さえる。 |
|
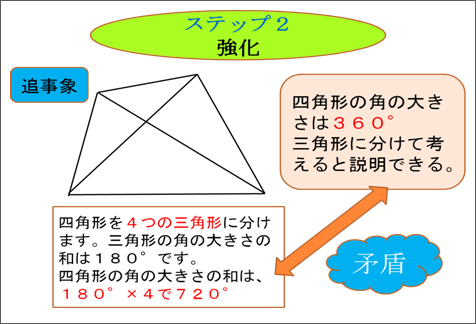
○4つの三角形に分けた四角形でも角の大きさの和が360°であることが説明できないか話し合う。(強化)
・真ん中のいらないところがあるから、720°から360°をひかないといけない。720-360=360 |
○2本の直線で4分割された四角形や3つの三角形に分割された四角形を追事象として提示し、この分け方では四角形の内角の和の認め方が説明できないか問いかける。 |
|
|
ま |
4.本時学習を振り返り、まとめる。 |
○四角形の内角の和が何度といえるか、それは何を使って説明できたかを振り返る。 |
|
四角形の角の大きさの和は360°である。四角形を三角形に分けて考え、三角形の角の大きさの和が180°である事を使って説明できる。 |
||
(2) 指導の実際(わかる段階・つかいこなす段階を中心に)
①わかる段階
【ステップ1】…見通しをもつ |
【ステップ2】…適用する |
【ステップ3】…習熟する |
②使いこなす段階
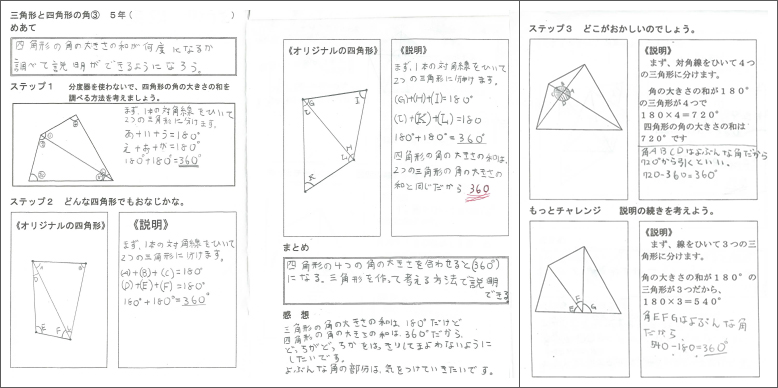
使いこなす段階では、まずステップ1でグループでの発表や代表児童の説明をする場を設定し、どんな四角形でも内角の和が360°になる事を確認した。つぎにステップ2として追事象の四角形を4つの三角形に分けた図形カードを提示した。この分け方では4つの三角形の角の大きさの和が180°×4=720°になる。本時では「どこがおかしいのか」という課題の与え方をしたが、「これも三角形に分けているが、この分け方では四角形の角の大きさの和は求められないか」という視点で交流させた方が良かったのではないかと考える。
子どもたちは図形カードを指しながら、四角形の角の大きさと関係がない角の大きさが含まれていることを見つけ、交流を進める中で、720°から、四角形の角には含まれない余分な角の大きさを取りのぞくことで、四角形の角の大きさの和が見つけられることを見出していった。さらに、3つの三角形に分割した四角形も、32名中29名が助言なしで自力で正しく説明をすることができていた。また、次の時間の12/15時の多角形の角の大きさの和を求める際も、全員の子供が戸惑うことなく三角形に分割して多角形の角の大きさの和を効率よく求めることができ、1単位時間内にn角形の角の大きさの和が(n-2)×180で求められるという規則性まで導き出すことができた。これらのことから、本時の習得の授業スタイルでの展開で、子どもたちは本時の学習内容を確実に理解し習得することができたと考える。
(3) 子どもの学習ノート
①11/15本時の学習ノート
②12/15時の学習ノート
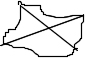 ○360°になっていることを4つの角を移動させ確認する。
○360°になっていることを4つの角を移動させ確認する。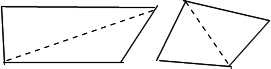
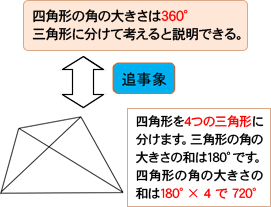
 ・3つの三角形に分けた四角形の角の大きさの和も説明できそう。
・3つの三角形に分けた四角形の角の大きさの和も説明できそう。