小学校 算数
小学校 算数

1.単元名
単位量あたりの大きさ(第5学年)
2.単元の目標
こみぐあいや人口密度、速さといった単位量あたりの大きさの意味や、異種の二つの量の割合として捉えられる数量は、単位量あたりの大きさを用いることで比べたり表したりできることを理解すること。
異種の二つの量の割合として捉えられる数量の関係に着目し、目的に応じて大きさを比べたり表現したりする方法を考察し、単位量あたりの大きさを求めたり、日常生活に生かしたりすること。
3.評価規準
こみぐあいや人口密度、速さといった単位量あたりの大きさの意味及び表し方について理解し、単位量あたりの大きさを求めることができる。
異種の二つの量の割合として捉えられる数量の関係に着目し、目的に応じて大きさを比べたり表現したりする方法を考察し、それらを日常生活に生かしている。
異種の二つの量の割合として捉えられる数量について、数直線図や式を用いて数学的に表現・処理したことを振り返り、多面的に捉え、検討してよりよいものを求めて粘り強く考えたり、数学のよさに気づき学習したことを生活や学習に活用したりしている。
4.本単元の指導にあたって
(主に「速さ」の内容に関して)
本学級の子どもたちは、これまでに50m走や持久走の練習においてかかった時間と道のりから速さを認識することができるようになっている。そこで、時間や道のりを基準として速さを比較することができるようになるこの期に本単元を取り上げる。そして、異種の二つの量の組み合わせとして捉えることができる速さを、時間と道のりといった二つの量の関係から単位量あたりの大きさで比較することができるようにする。
また、本単元の指導にあたっては、異種の二つの量の割合として捉えられる数量の関係に着目し、目的に応じて大きさを比べたり表現したりすることができるようにする。そのために、身の回りの速さの仕組みや速さを用いて道のりや時間を求める方法について調べていく中で、分かっている量を数直線に整理してそれらの関係に着目して調べていく教材を取り上げる。
そして、デジタル教材の効果的な活用場面としては、時間と道のりの関係で速さが決まることを、視覚的に捉えさせる場面で活用する。
5.単元の指導計画
時 |
学習のねらい |
おもな学習内容 |
|---|---|---|
1 |
二つの量の大きさが揃っていないときには、一方の大きさに揃えると比べることができることを捉える。 |
シートの数と子どもの人数の関係を数直線図に表し、シート□枚あたりの人数や、□人あたりのシートの数でこみぐあいを比べる。 |
3 |
1㎢あたりの人口を人口密度といい、人口密度でこみぐあいを表すことができることを捉える。 |
1㎢あたりにおよそ何人の人が住んでいるのかを、概数で表す。 |
4 |
異種の二つの量の割合として捉えられる数量は、単位量あたりの大きさに表すと簡単に比べることができることを捉える。 |
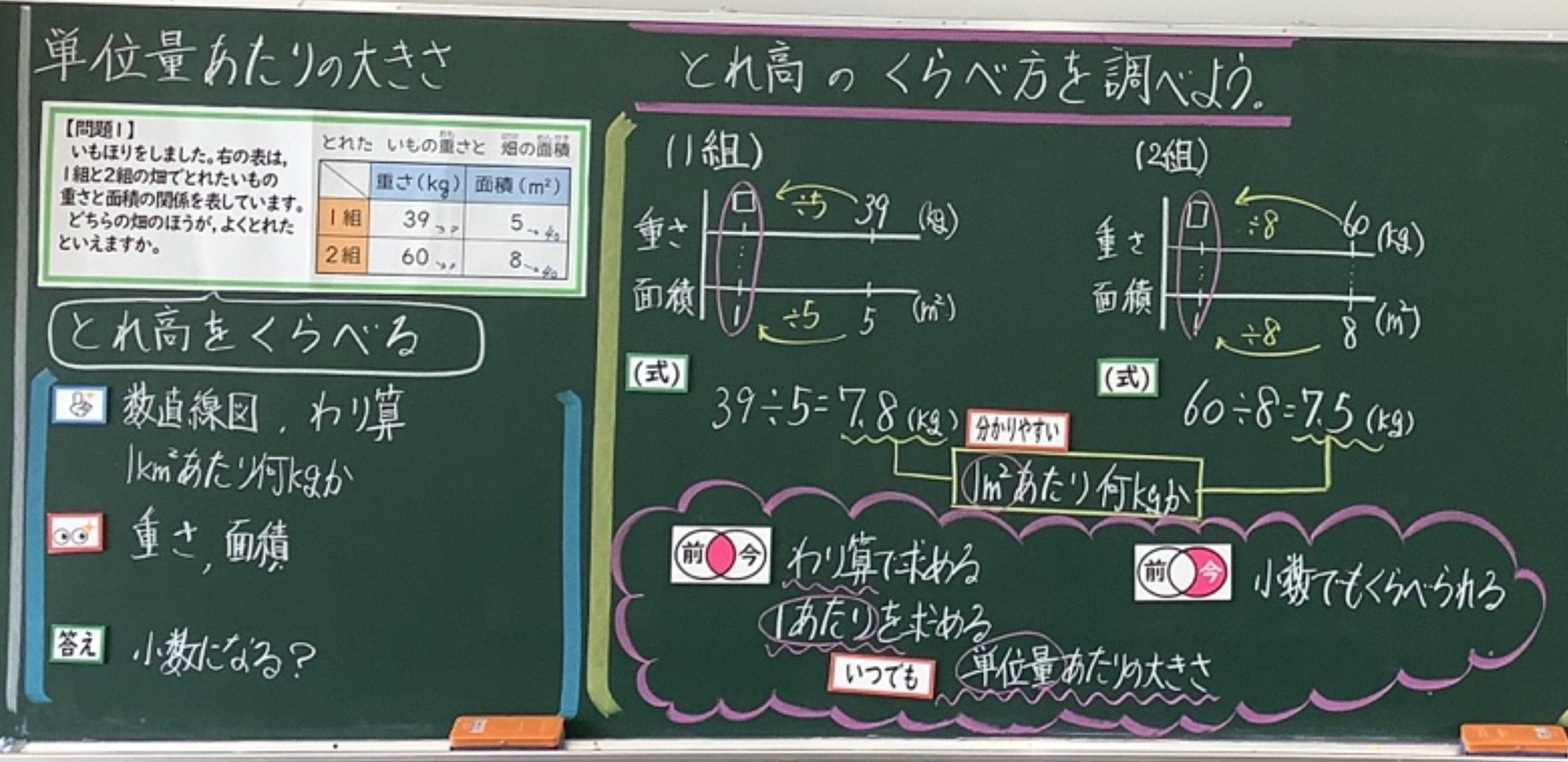
ある畑でとれたいもの重さと面積の関係を数直線図に表し、1㎡あたりの重さで、いものとれ高を比べる。 |
5 |
単位量あたりの大きさを用いて、問題解決の仕方を考えることができる。 |
針金1mあたりの重さを用いて、□mの重さや、△gの長さを求める。 |
6 |
速さは、単位時間あたりに進む道のりや、単位道のりあたりにかかる時間に揃えると比べることができることを捉える。 |
道のりと時間の関係を数直線図に表し、1分あたりの道のりや、1mあたりの時間で速さを比べる。 指導者用デジタル教材活用 |
7 |
速さは、単位時間あたりに進む道のりで表すことができることを捉える。 |
道のりと時間の関係を数直線図に表し、1時間あたりの道のりや、1kmあたりの時間で速さを表す。 指導者用デジタル教材活用 |
8 |
道のりは、速さに時間をかけることで求めることができることを捉える。 |
速さ(1時間あたりに進む道のり)と、かかった時間の関係を数直線図に表し、道のりの求め方を式に表す。 |
9 |
時間は、道のりを速さで割ることで求めることができることを捉える。 |
速さ(1分あたりに進む道のり)と進んだ道のりの関係を数直線図に表し、時間の求め方を式に表す。 |
10 |
仕事の速さは、仕事の量を時間で割ることで求めることができることを捉える。 |
仕事の量と時間の関係を数直線図に表し、単位時間あたりの仕事の量で仕事の速さを比べる。 |
11 |
時間と道のりや、時間と仕事の量の関係に着目し、身の回りのものの速さを求めることができる。 |
身の回りのいろいろなものの速さを調べ、レポートにまとめる。 |
6.本時の学習
速さは、単位時間あたりに進む道のりや単位道のりあたりにかかる時間に揃えると比べることができることを捉えることができるようにする。
(1)導入段階
この段階では、時間も道のりも揃っていないときの速さの比べ方を調べたいというめあてを持たせることをねらいとした。
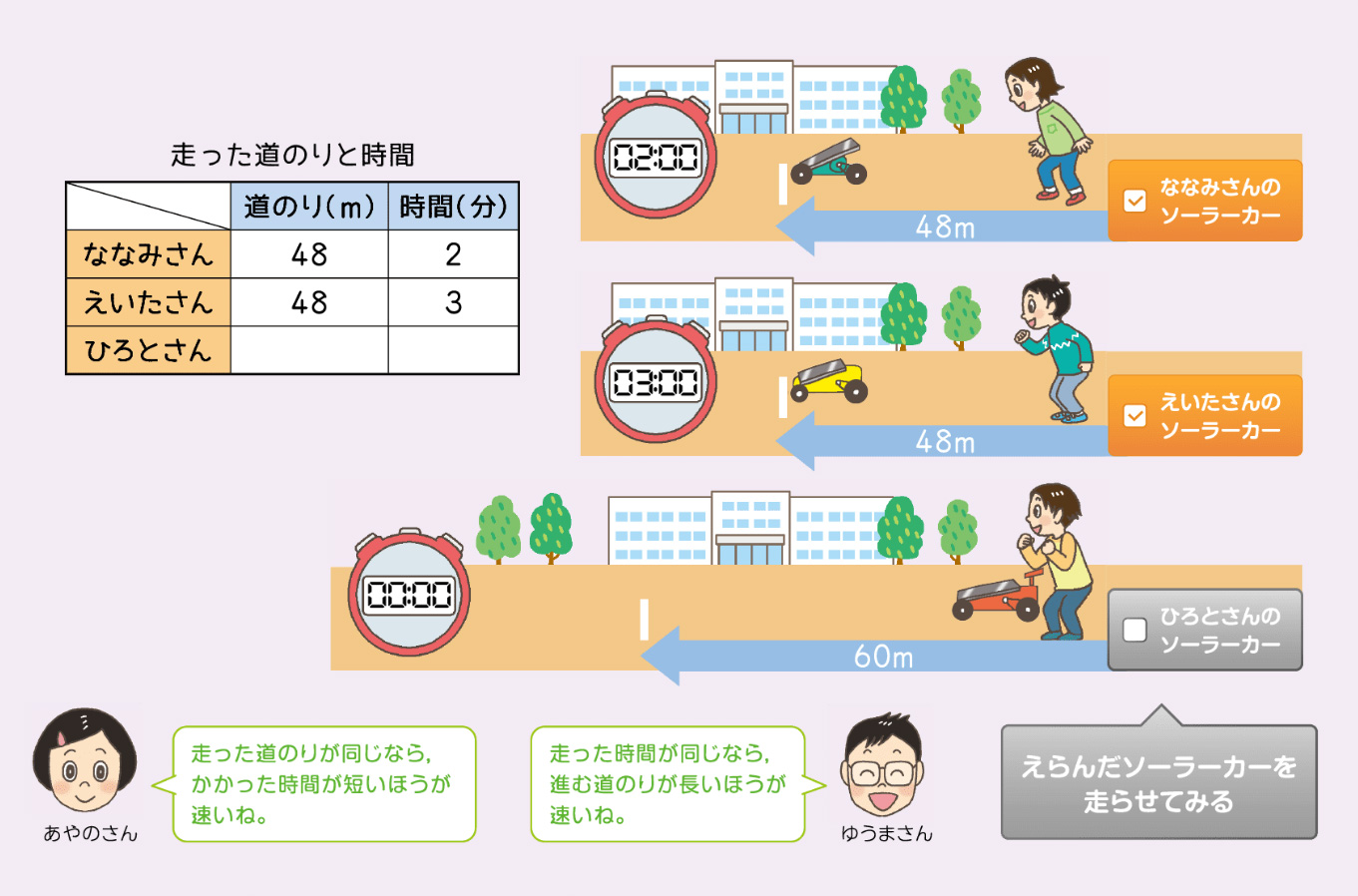
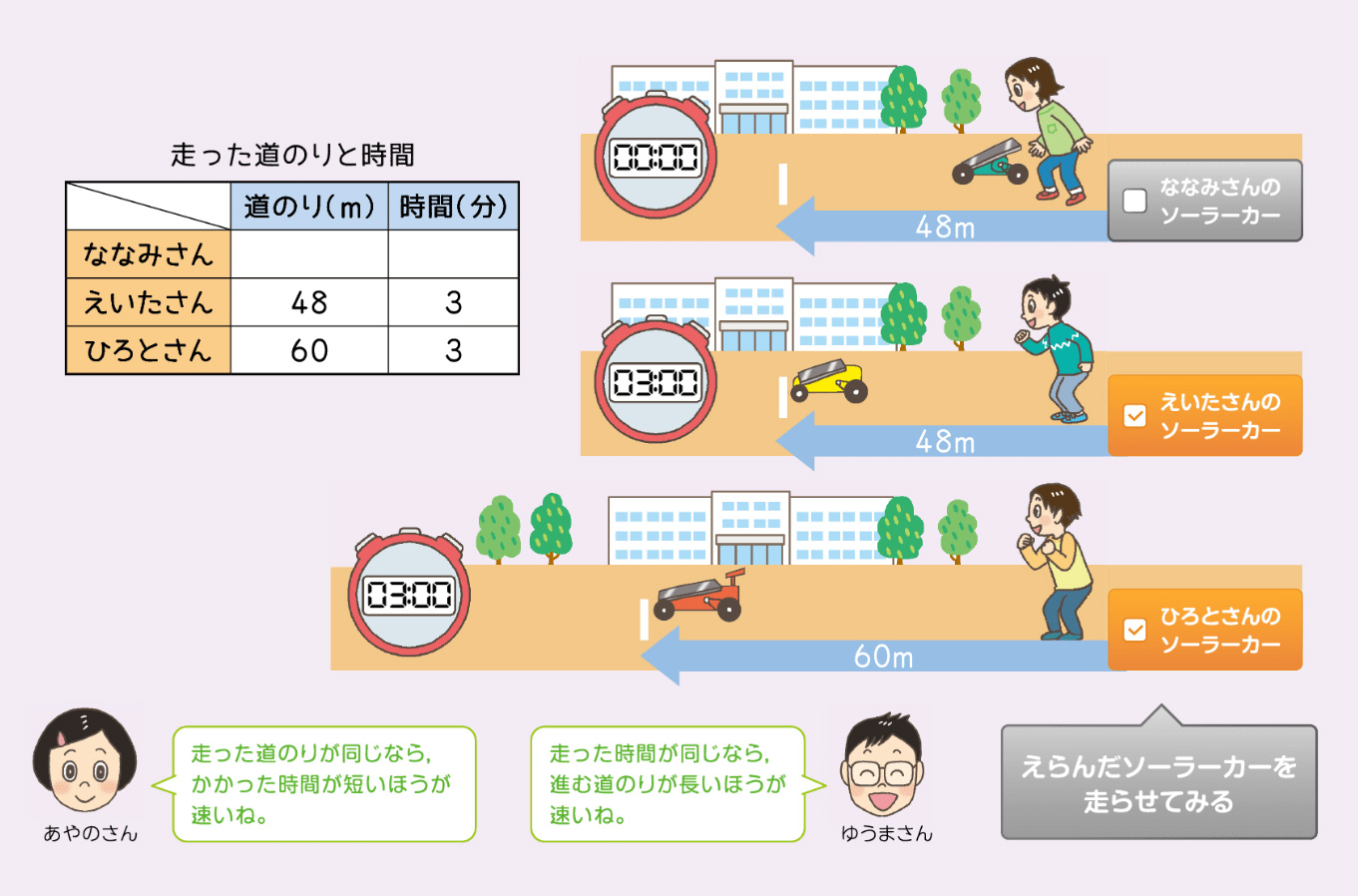
そのために、まず、ななみさんのソーラーカー(48m進むのに2分間かかる)とえいたさんのソーラーカー(48m進むのに3分間かかる)速さを比べたり(画像1)、えいたさんのソーラーカー(48m進むのに3分間かかる)とひろとさんのソーラーカー(60m進むのに3分間かかる)の速さを比べたり(画像2)する活動を位置づけた。
ここでは、デジタル教材のコンテンツを活用して、実際にソーラーカーが動く様子を視覚的に捉えさせ、速さを実感させることができるようにした。
子どもたちは、「道のりが揃っているときには、かかる時間が短い方が速い」、「時間が揃っているときには、進む道のりが長い方が速い」ことを捉えることができた。
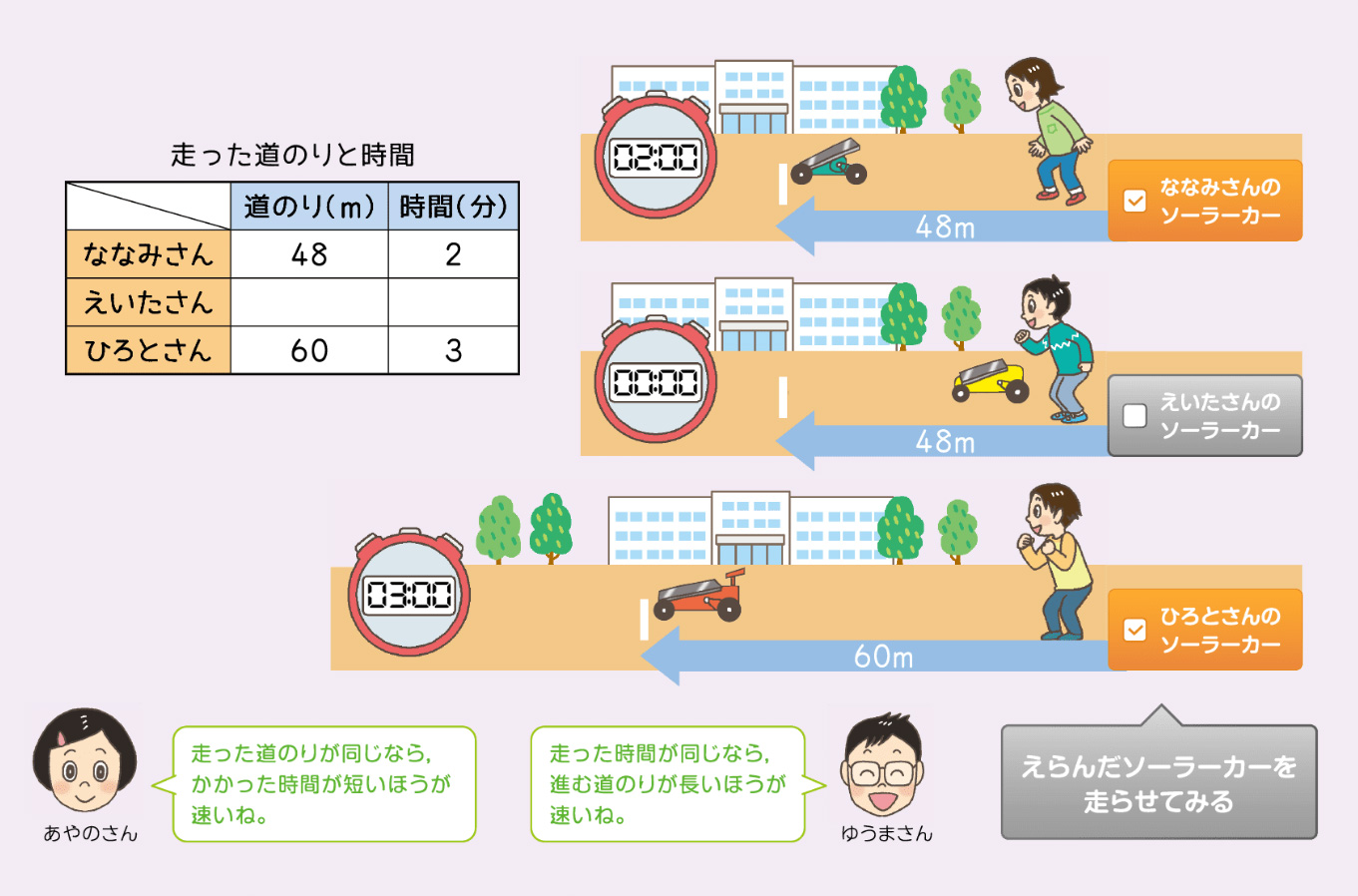
次に、ななみさんのソーラーカー(48m進むのに2分間かかる)とひろとさんのソーラーカー(60m進むのに3分間かかる)の速さを比べる(画像3)活動を位置づけた。ここでも、デジタル教材のコンテンツを活用して、実際にソーラーカーが動く様子を視覚的に捉えさせ、道のりと時間が揃っていない場合は、視覚的にもどちらが速いか判断できないことに気づかせることができるようにした。
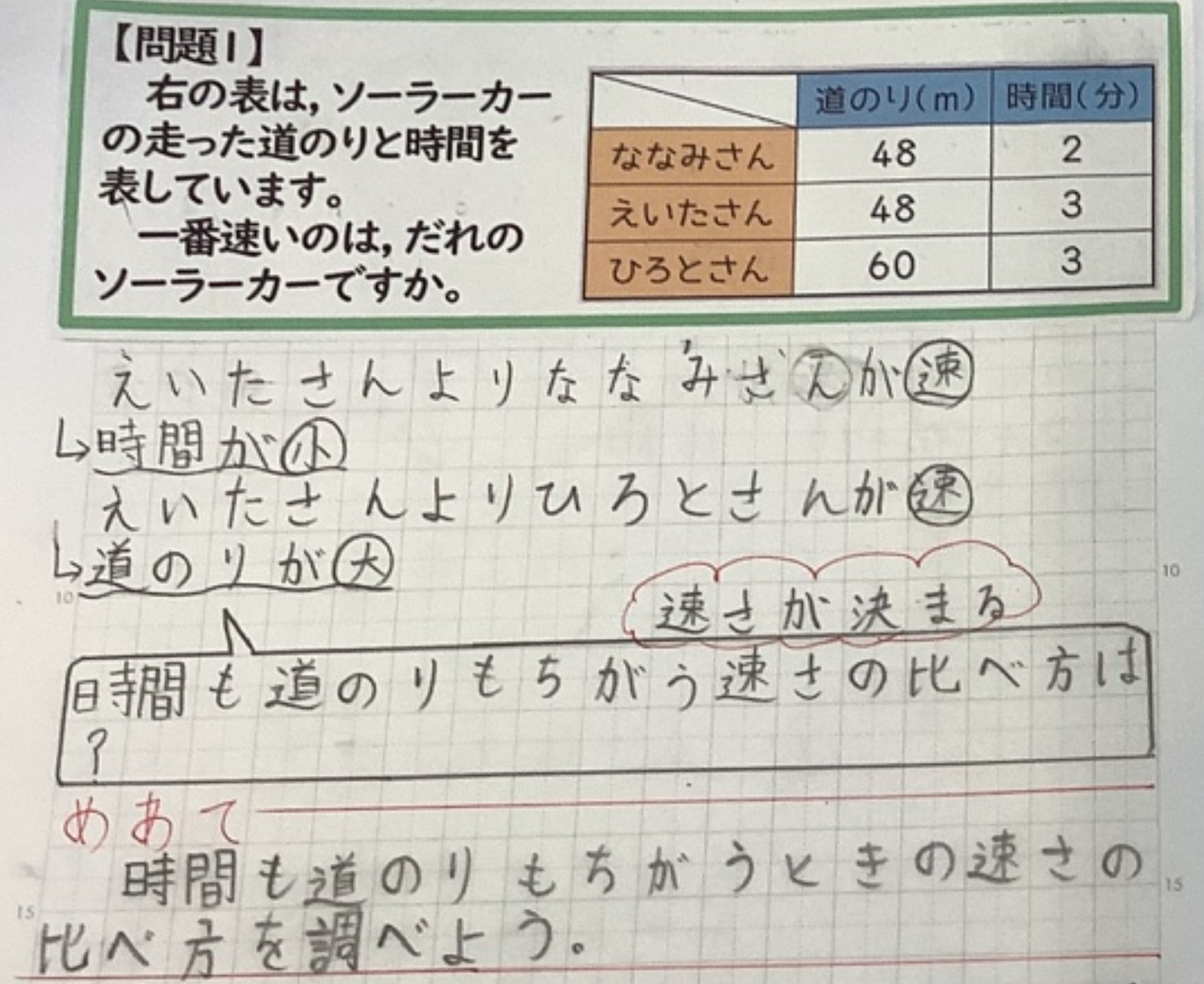
子どもたちは、「ななみさんとえいたさんの速さ比べ」や「えいたさんとひろとさんの速さく比べ」と、「ななみさんとひろとさんの速さ比べ」の活動を通して、「道のりや時間が揃っているときは速さが比べることができた」ことと、「速さと時間が揃っていないときには速さが比べられなかった」ことから、「時間も道のりも揃っていないときの速さの比べ方を調べたい」(画像4)というめあてを持つことができた。
この段階では、時間も道のりも揃っていないときの速さの比べ方を明らかにすることをねらいとした。
そのために、まず、既習の「とれ高を比べる」学習の「単位量あたりの大きさで比べた」問題場面から類推して立てた着目点や解決方法の見通しをもとに(画像5)、本時問題の見通しを立てて(画像6)、速さを比べる活動を位置づけた。
ここでは、子どもがICT機器を活用することで、保存していた前時までの板書や自他のノートを見直して類推的思考を働かせたり、友だちの解決方法を参考にして自分の考えを付加・修正・強化したりすることができるようにした。
子どもは、既習のとれ高を比べる問題場面から類推して、「時間」と「道のり」の二つの量に着目し、「数直線」「1分間か1mに揃える」といった方法の見通しを持って問題を解決することができた(画像7)。
次に、全体で、共通点を観点に、「1分間あたりの道のりで比べる方法」と「1mあたりの時間で比べる方法」を比較し、速さの比べ方を見いだす活動を位置づけた。
子どもは、前時までの「単位量あたりの大きさで比べる方法」を根拠に、速さを比べるときには「時間や道のりを単位量あたりの大きさで揃えると比べることができる」ことを見いだすことができた。
この段階では、時間も道のりも揃っていないときの速さを比べるときには、単位時間あたりに進む道のりや、単位道のりあたりにかかる時間を求めると比べることができることを確かめることをねらいとした。
そのために、みおさんのソーラーカー(3分間で69m進む)の速さを求めて、ほかの3人のソーラーカーの速さと比べる「ためしてみよう」を解決し、本時の学習内容をまとめる活動を位置づけた。
子どもは、速さを比べるときには、単位時間あたりに進む道のりや単位道のりあたりにかかる時間に揃えることで比べることができることを捉えることができた。
7.指導を終えて
本単元に関するデジタル教材の活用については、単元を通して効果的な活用場面が2つあった。
1つは、本時「速さを視覚的に捉える場面」である。異種の二つの量の割合として捉えられる数量の中でも、こみぐあいや人口密度、とれ高に比べて、速さは視覚的に捉えにくい。そこで、デジタル教材の中にある、速さを視覚的に捉えることができるコンテンツを活用した。これは、子どもが速さを視覚的に捉えることができ、子どもの速さの概念を確かにする上で効果的であった。また、道のりや時間の一方が揃っている場合には比べることができ、揃っていないときには比べにくいことを実感させる上でも効果的であった。
もう1つは、次時「問題場面を数直線上に表す場面」である。ここでは、デジタル教材の中にある、問題場面の数値が数直線上に移動する様子を動的に表しているコンテンツを活用した。これは、数直線上にある数値が、問題場面のどの数値と対応しているのかを理解する上で効果的であった。また、時速□kmという数値には、「1時間あたりに□m進む」という意味があり、数直線上に表す場合は、2つの数値になることを捉えさせる上でも効果的であった。
本時学習におけるICT機器の活用としては、ICT機器の「保存機能」と「共有機能」を活用した。
保存機能に関しては、既習の板書や自他のノートを写真としてタブレット端末に保存していたことで、子どもが見通しを立てる際に、既習の問題場面から類推して考えることができた。このことは、これまでの、既習の図を用いて振り返りをさせたり、ノートを見返したりすることに比べて、効率的に活動を進めることができた。
共有機能に関しては、自他の解決方法を写真に撮って学級で共有したことで、子どもは、友だちの解決方法を参考にして自分のつくった解決方法を見直し、自分の解決方法を付加・修正・強化することができた。このことは、これまでの、ペアで解決方法を説明し合ったり、自分の解決方法とは違う解決方法の友だちを見つけて紹介し合ったりすることに比べて、効率的に活動を進めることができた。
本時学習の振り返りとして、子どもは、「1分あたりに進む道のり」や「1mあたりにかかる時間」で速さを比べることができることを捉えることができていた(画像8)。
また、本時で新たに着目した点として、「道のり」と「時間」の2つを挙げていた。
これは、デジタル教材のコンテンツを活用して、速さを視覚的に捉えることができたことの効果があったと考える。
さらに、既習との共通点としては、やはり数直線を活用することの有効性を実感することができていた。