小学校 算数
小学校 算数

1.単元名
割合「比べ方を考えよう」(第5学年)
2.単元の目標
⑴ある二つの数量の関係と別の二つの数量の関係とを比べる場合に割合を用いる場合があることを捉え、百分率を用いて表したり、割合などを求めたりすることができる。(知識及び技能)
⑵日常の事象における数量の関係に着目し、図や式などを用いて、ある二つの数量の関係と別の二つの数量の関係との比べ方を考察し、それを日常生活に生かすことができる。(思考力、判断力、表現力等)
⑶割合を用いた比べ方のよさを感じて、学習や生活に生かそうとしているとともに、考察の方法や結果を批判的に振り返り、よりよく問題を解決しようとしている。(学びに向かう力、人間性等)
3.評価規準
○ある二つの数量の関係と別の二つの数量の関係とを比べる場合に割合を用いる場合があることを理解している。
○百分率を用いた表し方を理解し、割合などを求めることができる。
○日常の事象における数量の関係に着目し、図や式などを用いて、ある二つの数量の関係と別の二つの数量の関係との比べ方を考察し、それを日常生活に生かしている。
○二つの数量の関係について、数学的に表現・処理したことを振り返り、多面的に捉え検討してよりよいものを求めて粘り強く考えたり、数学のよさに気付き学習したことを生活や学習に活用しようとしたりしている。
4.本単元の指導にあたって
子どもは、第4学年において、簡単な場合について割合を用いる経験をしてきている。そこでは、二つの数量の関係に着目し、図や式を用いて、二つの数量の関係どうしの比べ方を考察してきた。このような子どもが、割合が小数で表される場合に考察の対象を広げれば、百分率を用いた表し方を捉え、値下げ率や打率などの割合を求めることができるようになるだろう。
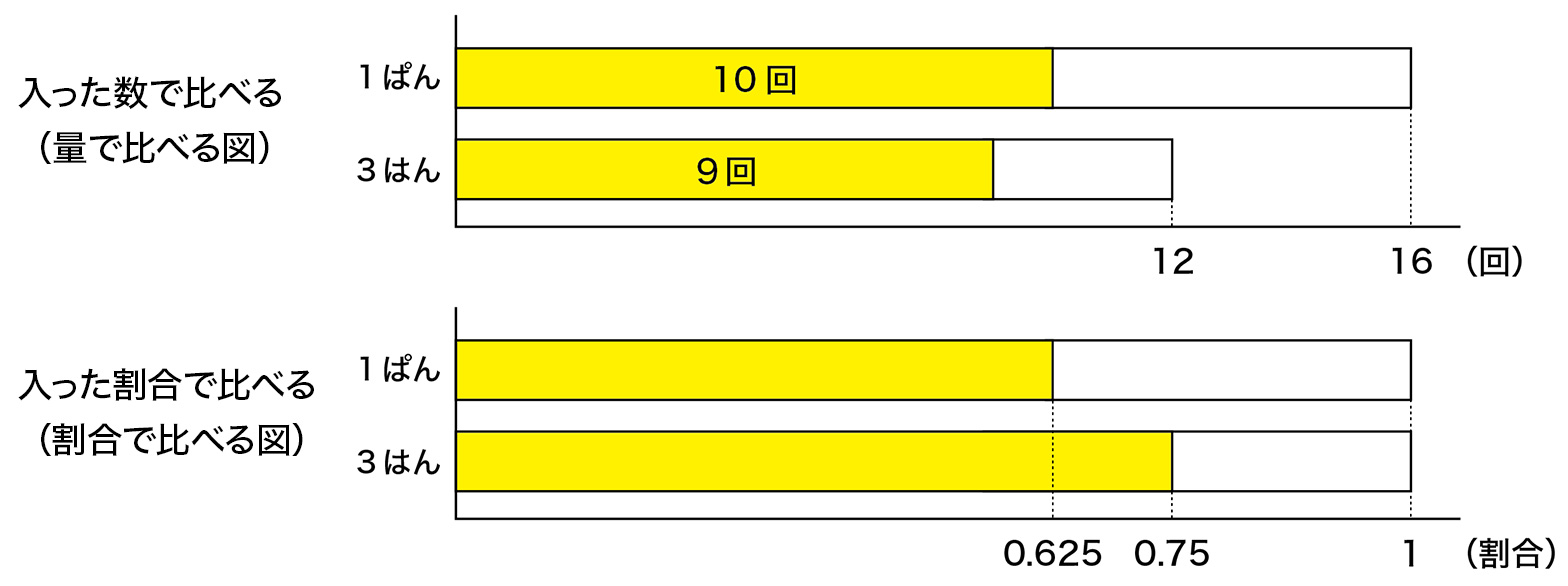
本単元は、割合が小数で表される場合においても、二つの数量の関係に着目し、図や式を用いて、二つの数量の関係どうしの比べ方を考察し、日常生活に生かす力をのばすことをねらいとしている。割合の意味の指導においては、日常生活で二つ以上の事象の大きさを比べる場面で、量で比べる場合と割合で比べる場合があることを捉えさせ、場面に応じて適切に判断できるようにすることが大切である。そこで、輪投げの記録を使って「一番うまく投げられた班」を探る活動を設定する。子どもは、輪投げをした回数が異なる場合は、入った数で比べるのではなく、「(入った数)÷(投げた数)」という割合で比べる方が適切であると判断していくだろう。その際、下のような図1を用いて、量で比べる場合と割合で比べる場合の違いを明らかにすることが大切である。
そうすることで、割合が小数で表される場合においても、比べる対象を明確にし、比べるために必要となる二つの数量の関係を、比例関係を前提に、割合でみてよいかを判断する力を養うことができると考える。
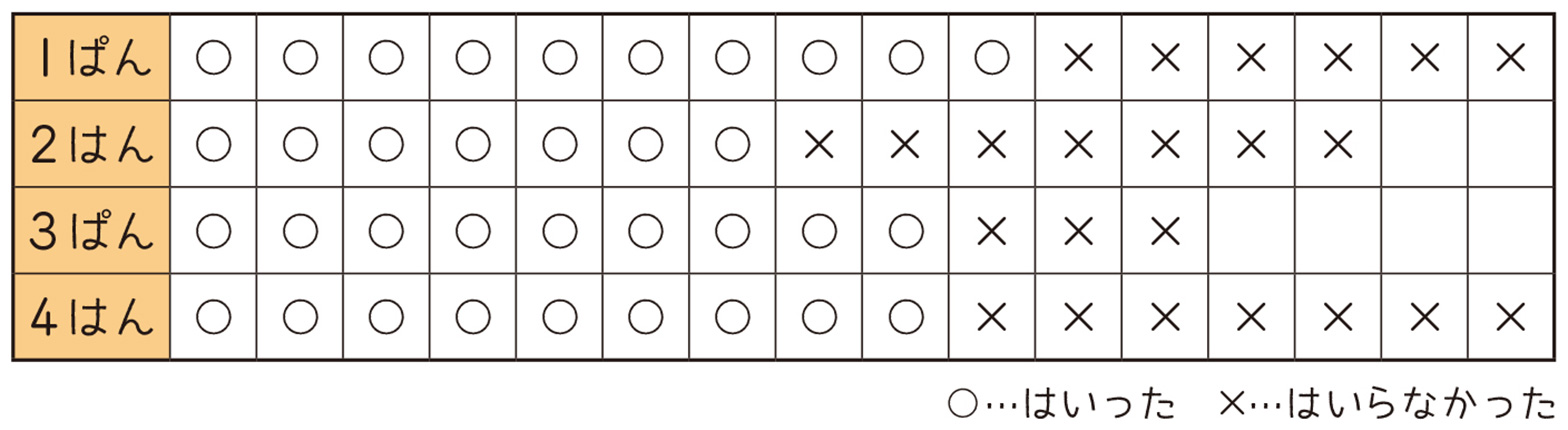
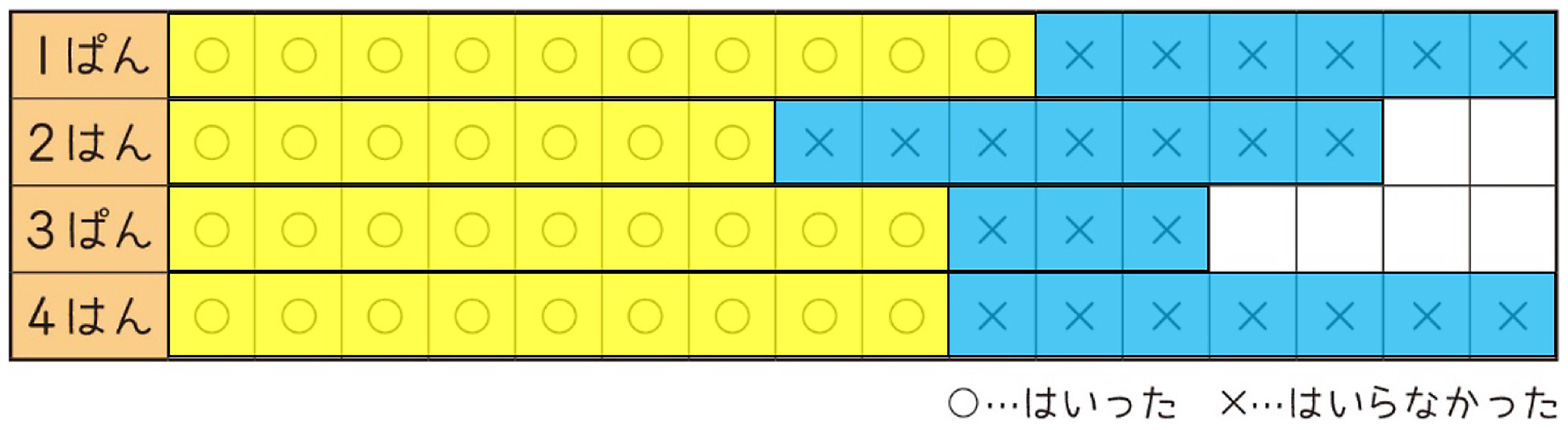
図1において、(量で比べる図)から(割合で比べる図)へと変化していく様子を、子どもに視覚的に訴えることができれば、その二つの違いをより明らかにすることができると考える。そこで、プレゼンテーションアプリに、データの画像(画像1)を挿入し、長方形の図形で加工したスライド(画像2)を一人一台タブレットに配付し使用させる。子どもは、各々の操作で長方形の図形を横方向に拡大することにより大きさをそろえるだろう(画像3)。そうすることで、(量で比べる図)から(割合で比べる図)へと変化していく様子を体感し、その二つの違いをより鮮明に捉えることができると考える。
5.単元の指導計画
時 |
学習のねらい |
おもな学習内容 |
|---|---|---|
1 |
輪投げ大会で一番うまく投げられた班を探る活動を通して、割合で比べる方法を見いだすことができる。 |
・同種の2量の大きさの比べ方 デジタル教科書 |
2 |
4年で学んだ割合と比較する活動を通して、割合が小数の場合でも使えることを見いだすことができる。 |
・小数で表す割合の意味の拡張 デジタル教科書 |
3 |
2本数直線図を用いて割合を求める活動を通して、割合の求め方をことばの式としてまとめることができる。 |
・割合の求め方の公式化 デジタル教科書 |
4 |
日常から割合の便利な表現を探る活動を通して、百分率の意味を捉え、割合を百分率で表すことができる。 |
・百分率の意味と表し方 デジタル教科書 |
5 |
日常から割合の便利な表現を探る活動を通して、歩合の意味を捉え、割合を歩合で表すことができる。 |
・歩合の意味と表し方 デジタル教科書 |
6 |
2本数直線図を用いて比べる量を求める活動を通して、比べる量の求め方をことばの式としてまとめることができる。 |
・比較量の求め方の公式化 デジタル教科書 |
7 |
2本数直線図を用いてもとにする量を求める活動を通して、もとにする量の求め方をことばの式としてまとめることができる。 |
・基準量の求め方の公式化 デジタル教科書 |
8 |
割引された代金の求め方を探る活動を通して、割引の意味について説明することができる。 |
・定価、割合、代金の関係 デジタル教科書 |
9 |
お得な店はどちらかを探る活動を通して、2割引きと30円引きの計算の仕方の違いを捉えることができる。 |
・様々な割引表記 デジタル教科書 |
6.本時の学習
輪投げ大会で一番うまく投げられた班を探る活動を通して、割合で比べる方法を見いだすことができる。
導入の場面
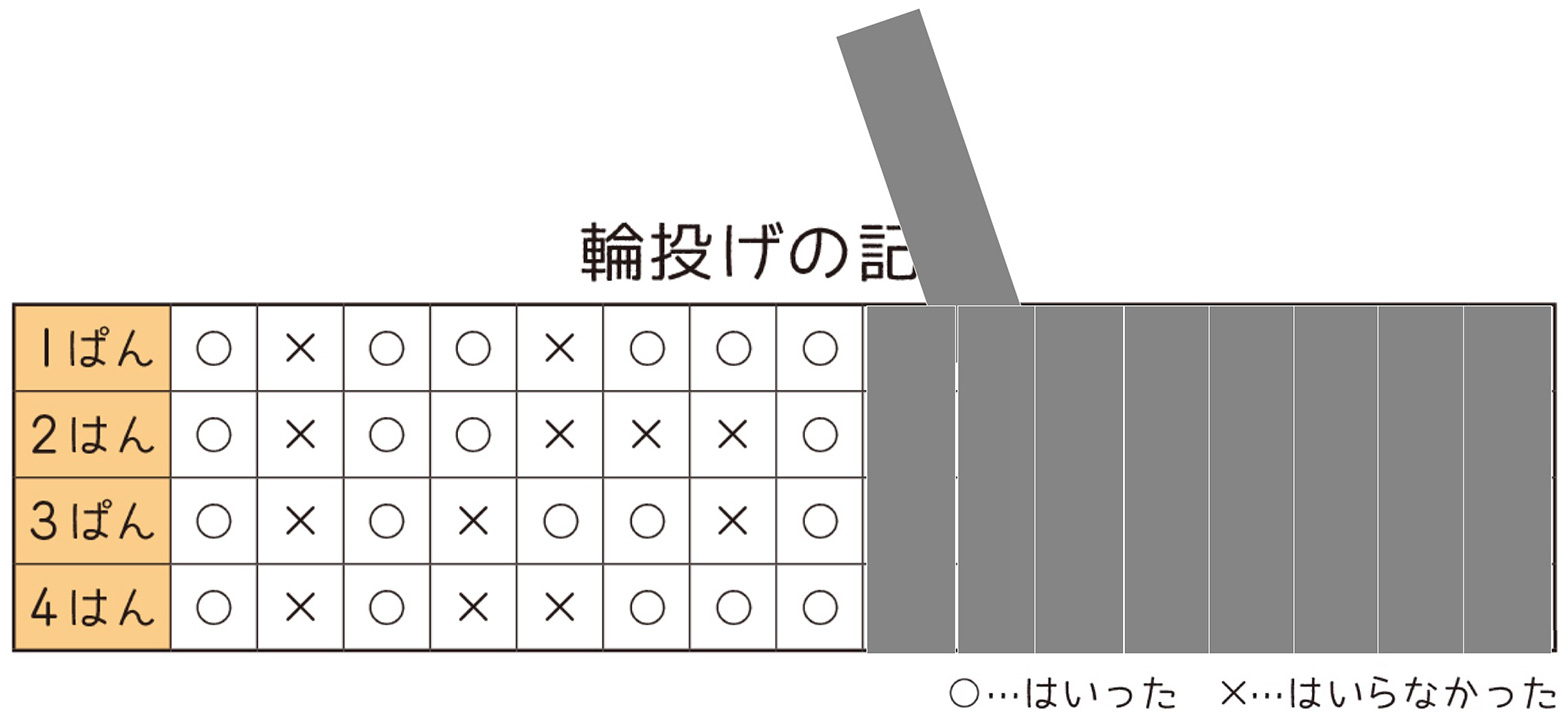
本時のめあてを「輪投げのうまさを比べる方法を見つけよう」と提示する。問題把握に必要なデータだけを厳選して提示した。特に、輪投げの記録は、いきなり全部を見せるのではなく、画像4のように一投ずつの結果を見せていった。
そうすることで、子どもは問題場面に興味を抱いて集中し、短時間で本時のポイントとなる「投げた回数が揃っていないこと」に着目し、そのまま自力解決に入ることができた。
自力解決では、導入場面と同じデータを挿入したプレゼンテーションアプリを子どもに配付し、ノートと併用して自由に使ってよいことを指示した。
そうすることで、ほとんどの子どもがタブレット上に書き込みを行い、画像5や画像6のように、自分の考えを形成するための試行錯誤を、繰り返し行うことができた。子どもは、行き詰まるとリセットしてすぐにやり直したり、スライドをコピーして増やして別解を導こうとしたりする姿が見られた。色を変えながら書き込み、思考を整理しようとする姿も見られた。
以下は自力解決後の学び合いの様子である。(T:教師、C:子ども)
T:どの班が一番うまかったのだろう?
入った数 |
投げた数 |
|
|---|---|---|
1ぱん |
10 |
16 |
2はん |
7 |
14 |
3はん |
9 |
12 |
4はん |
9 |
16 |
C:入った数は2班が一番少ないので、2班がうまいとは言えないと思います。
C:単純に考えたら、そう言えるかもしれないけど、投げた数がそろってないから、それじゃあ比べられないと思います。
C:僕は、この前(の単元の学習)の単位量あたりで1㎡に何人いるかでそろえたと思うんですけど、また、そろえたらできると思います。
C:僕も、そろえてみようと思ってやってみたんだけど、難しかった。
T:何をそろえたいんだろう?
C:投げた数をそろえればよいのではないでしょうか?
C:入った数もいると思う。
C:なら、分数にして通分すればよいと思う。
C:分数にしても、もとにする量が違うからできないのでは?あっ、でも通分すればできるね。
T:どんな分数になるのかな?
C:1班は10/16、2班は7/14、3班は9/12、4班は9/16となります。
T:これらの分数の意味を教えてほしい。
C:分母は投げた数で、分子が入った数です。
T:でも、これじゃあ、まだ比べられないね。
C:この前習ったことを活かして小数にすればよい。
C:1班は10/16=10÷16=0.625、2班は7/14=7÷14=0.5、3班は9/12=9÷12=0.75、4班は9/16=9÷16=0.5625
C:この中で数値が一番大きいのは0.75だから、一番投げるのが上手いのは3班だと思います。
T:通分して比べていた人もいたね。教えてください。
C:1班が210/336、2班が168/336、3班が252/336、4班が189/336
T:336回で252回入った3班が、一番上手いことがわかるね。
C:僕は約分して更に通分しました。すると、1班が10/16、2班が8/16、3班が12/16、4班が9/16となり、3班が一番上手なことがわかりました。
この後は、めあてに立ち戻り、上手さを比べるには、「もとにする量をそろえれば比べることができる。」とまとまった。
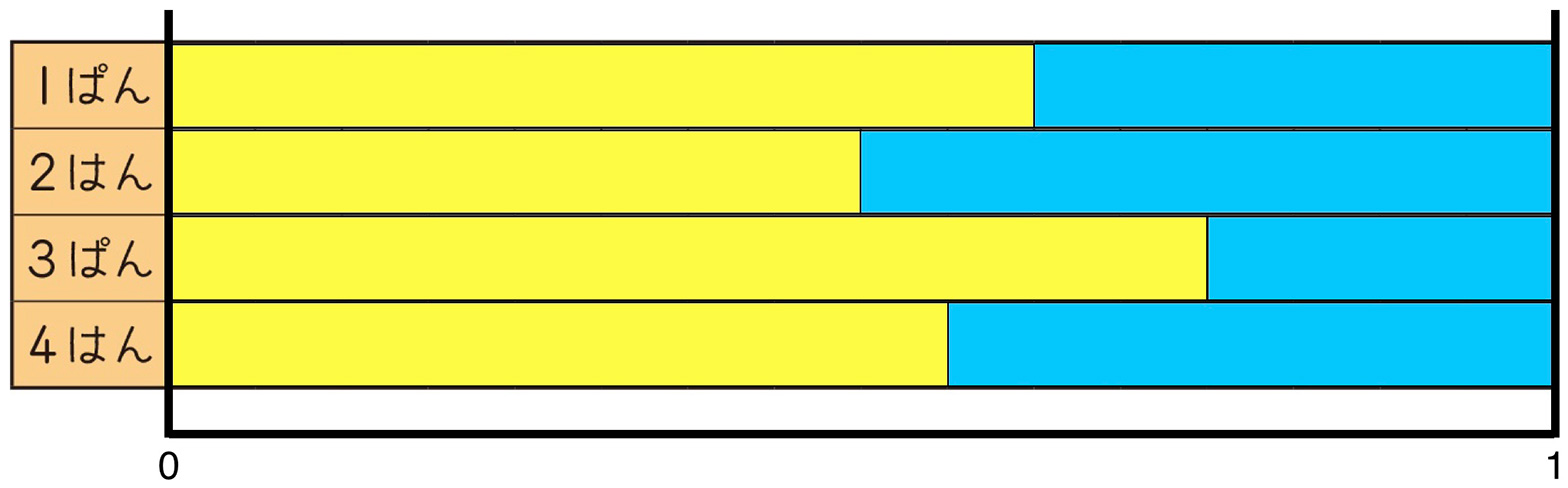
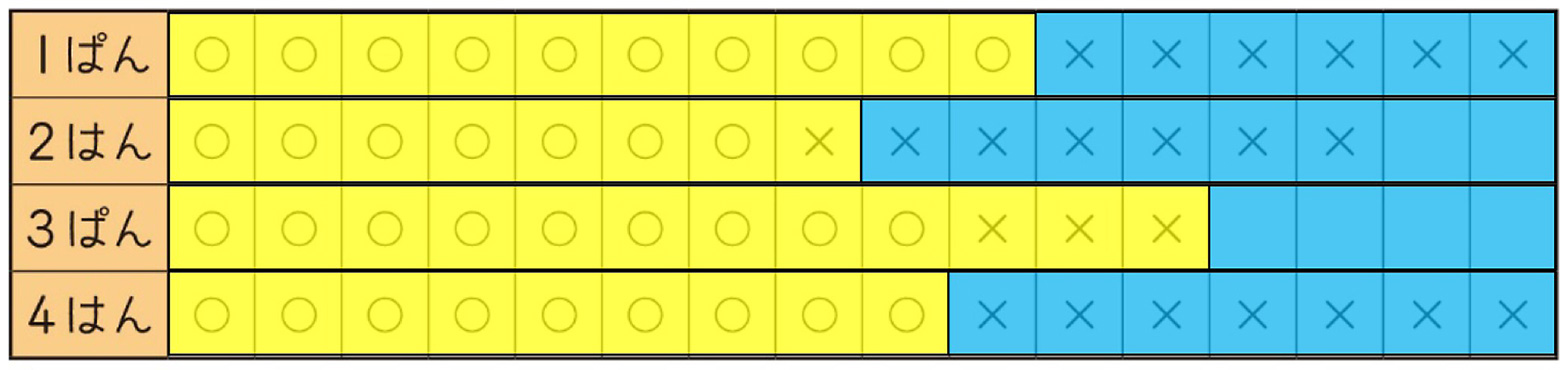
子どもたちに、「図に戻ってみよう。今のことが、図から見えないかな?」と、問いかける。そこで、画像8のようにタブレットを操作させ、画像9の状態を作らせた。
画像9を使って、1班が10/16、2班が8/16、3班が12/16、4班が9/16となっていることを確認すると、子どもたちから感嘆の声がもれる。
T:この図からも3班であることがわかりますね。数値もですが、図とも重ね合わせながら、これからの学習を進めていきましょうね。
7.指導を終えて
自力解決の際、子どもには数値を見せず、図だけを見せている。そうすることで、子どもは数値をむやみに足したり引いたりすることがなくなった。また、図と関連させながら数値に着目する姿も見られた。問題場面についてのイメージを膨らませながら、問題解決を行おうとしているからだろう。このような指導を積み重ねていけば、子どもは計算から出した答えの意味を自ら捉えるようになっていくと考えている。
同種の量の割合の指導では、次のような学習過程を踏んでいく。
①一方の数量をそろえて他方で比較する。
・公倍数の考え ・平均の考え
②一方を単位量として他方で数値化する。
・等分除的解釈 ・単位量あたりの考え
③一方(全体)を1とみて他方を測定して数値化する。
・包含除的解釈 ・測定の考え
本時では、子どもから①、②までの数学的アイデアが出てきたので、十分におさえることができた。しかし、③へのステップが不十分であった。本時の終末の場面において、子どもが導いた10/16や8/16などの分数と画像9を結び付けたことに満足せずに、小数の答え方にも触れて画像3へとつなげておけばよかった。せめて、基準量の1には触れておくべきだった。そうすれば、第2時において、1班:0.625や2班:0.5などの数値の意味を確認し、全体を1とみた割合の考えであることを捉える際に、子どもは単位量あたりで比べる場合と割合で比べる場合の違いを、より明らかにすることができたであろう。指導者としても、画像3と画像9の意味の違いを明らかにしておくことの大切さを学んだ実践であった。
【参考資料】
- 小学校学習指導要領(平成29年告示)解説 算数編
- 「指導と評価の一体化」のための学習評価に関する参考資料
- 平成29年度全国学力・学習状況調査報告書